题目内容
16.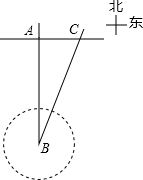 台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问:
台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问:(1)该城市是否会受到台风影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
分析 (1)过点A作AD⊥BC于D点,求出AD的长,比较即可得到答案;
(2)根据题意找出点E和点F,根据勾股定理求出EF的长,根据台风的速度求出时间;
(2)根据每远离台风中心25千米,台风就会减弱一级计算即可.
解答  解:(1)该城市会受到台风影响.
解:(1)该城市会受到台风影响.
理由:如图1,过点A作AD⊥BC于D点,则AD即为该城市距离台风中心的最短距离.
在Rt△ABD中,因为∠B=30°,AB=240.
AD=$\frac{1}{2}$×240=120(千米).
由题可知,距台风中心在(12-4)×25=200(千米)以内时,则会受到台风影响.
因为120千米<200千米,因此该城市将会受到“圣帕”影响.
(2))依题(1)可知,当点A距台风中心不超过200千米时,会受台风影响,
故在BC上作AE=AF=200;
台风中心从点E移动到点F处时,
该城市会处在台风影响范围之内.(如图2)
DE=160(千米).
所以EF=2×160=320(千米).
又知“圣帕”中心以20千米/时的速度移动.
所以台风影响该城市320÷20=16(小时).
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12-(120÷25)=7.2(级).
答:该城市受台风影响最大风力7.2级.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、灵活运用等腰三角形的性质和勾股定理是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
6.下列命题:
①若点P(x、y)满足xy<0,则点P在第二或第四象限;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④当x=0时,式子6-$\sqrt{9-{x}^{2}}$有最小值,其最小值是3;
其中真命题的有( )
①若点P(x、y)满足xy<0,则点P在第二或第四象限;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④当x=0时,式子6-$\sqrt{9-{x}^{2}}$有最小值,其最小值是3;
其中真命题的有( )
| A. | ①②③ | B. | ①③④ | C. | ①④ | D. | ③④ |
8.有下列各式(1)$\sqrt{{{(a+2b)}^2}}$=a+2b(2)$\sqrt{{x^2}-4}=\sqrt{x+2}•\sqrt{x-2}$(3)$\sqrt{\frac{3a}{b}}=\frac{1}{b}\sqrt{3ab}$,其中一定成立的有
( )
( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5.下列几何体中,主视图是等腰三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
 阅读下面的推理过程,在括号内填上推理的依据,如图:
阅读下面的推理过程,在括号内填上推理的依据,如图: 已知:如图,平行四边形ACBD中,对角线AC、BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.
已知:如图,平行四边形ACBD中,对角线AC、BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.