题目内容
1.计算:(1)$\sqrt{8}$+|$\sqrt{2}$-1|-π0+($\frac{1}{2}$)-1
(2)$({2\sqrt{5}-2\sqrt{3}})({\sqrt{12}+\sqrt{20}})$.
分析 (1)原式利用二次根式性质,绝对值的代数意义,零指数幂、负整数指数幂法则计算即可得到结果;
(2)原式变形后,利用平方差公式计算即可得到结果.
解答 解:(1)原式=2$\sqrt{2}$+$\sqrt{2}$-1-1+2=3$\sqrt{2}$;
(2)原式=(2$\sqrt{5}$-2$\sqrt{3}$)(2$\sqrt{5}$+2$\sqrt{3}$)=20-12=8.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.若m=$\sqrt{40}$-2,则估计m的值所在的范围是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |
10.有四条线段,长度分别是2cm,3cm,4cm,5cm,从中任取三条,能构成三角形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
11.点M(1-m,3-m)在x轴上,则点M坐标为( )
| A. | (0,-4) | B. | (4,0) | C. | (-2,0) | D. | (0,-2) |
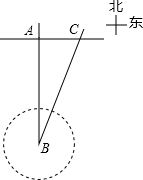 台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问:
台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问: 如图,已知∠AFB=∠CED,AF=CE,要使△ABF≌△CDE,应补充的直接条件是
如图,已知∠AFB=∠CED,AF=CE,要使△ABF≌△CDE,应补充的直接条件是 将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.
将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.