题目内容
6. 已知:如图,平行四边形ACBD中,对角线AC、BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.
已知:如图,平行四边形ACBD中,对角线AC、BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.(1)求证:四边形ABDF是平行四边形;
(2)若AB=BC=5.??
①求∠CAF的度数;?
②若BD=8,则△ABF的面积为12.??
分析 (1)由平行四边形的性质得出AB∥CD,AB=CD,再证出AB=DF,即可得出四边形ABDF是平行四边形;
(2)首先证明四边形ABCD是菱形,再用菱形的性质可得到AC⊥BD,再根据两直线平行,同位角相等得到∠CAF=∠COD=90°;
(3)由勾股定理求出OA,得出AC,△ABF的面积=$\frac{1}{2}$菱形ABCD的面积,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CD,
∴AB∥DF.
∵DF=CD,
∴AB=DF.
∴四边形ABDF是平行四边形.
(2)解:①∵四边形ABCD是平行四边形,且AB=BC,
∴四边形ABCD是菱形.
∴AC⊥BD.
∴∠COD=90°.
∵四边形ABDF是平行四边形,
∴AF∥BD.
∴∠CAF=∠COD=90°;
②∵四边形ABCD是菱形,
∴OA=OC,OB=OD=$\frac{1}{2}$BD=4,AC⊥BD,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AC=2OA=6,
∴△ABF的面积=$\frac{1}{2}$菱形ABCD的面积=$\frac{1}{2}$×$\frac{1}{2}$×8×6=12;
故答案为:12.
点评 此题主要考查了平行四边形的判定与性质,菱形的判定与性质,平行线的性质,解决问题的关键是熟练掌握平行四边形的判定方法与性质.

练习册系列答案
相关题目
17.在实数0,π,$\frac{1}{3}$,$\sqrt{2}$,-$\sqrt{9}$中,无理数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1. 如图,在平面直角坐标系中,三角形ABC的三个顶点的坐标分别为A(-2,5)、B(-4,3)、C(-1,1),请作出三角形ABC向右平移5个单位后得到的三角形A1B1C1,并求出三角形ABC的面积.
如图,在平面直角坐标系中,三角形ABC的三个顶点的坐标分别为A(-2,5)、B(-4,3)、C(-1,1),请作出三角形ABC向右平移5个单位后得到的三角形A1B1C1,并求出三角形ABC的面积.
 如图,在平面直角坐标系中,三角形ABC的三个顶点的坐标分别为A(-2,5)、B(-4,3)、C(-1,1),请作出三角形ABC向右平移5个单位后得到的三角形A1B1C1,并求出三角形ABC的面积.
如图,在平面直角坐标系中,三角形ABC的三个顶点的坐标分别为A(-2,5)、B(-4,3)、C(-1,1),请作出三角形ABC向右平移5个单位后得到的三角形A1B1C1,并求出三角形ABC的面积.
11.点M(1-m,3-m)在x轴上,则点M坐标为( )
| A. | (0,-4) | B. | (4,0) | C. | (-2,0) | D. | (0,-2) |
15.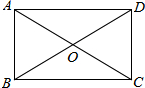 如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
 如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | OA=OB | D. | OA=AD |
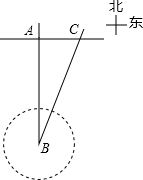 台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问:
台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问: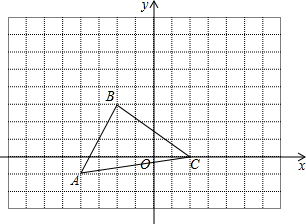 如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1.
如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1.