题目内容
4. 阅读下面的推理过程,在括号内填上推理的依据,如图:
阅读下面的推理过程,在括号内填上推理的依据,如图:因为∠1+∠2=180°,∠2+∠4=180°(已知)
所以∠1=∠4,(同角的补角相等)
所以a∥c.(内错角相等,两直线平行)
又因为∠2+∠3=180°(已知)
∠3=∠6(对顶角相等)
所以∠2+∠6=180°,(等量代换)
所以a∥b.(同旁内角互补,两直线平行)
所以b∥c.(平行与同一条直线的两条直线平行)
分析 依据同角的补角相等可证明∠1=∠4,依据平行线的判定定理可证明a∥c,依据对顶角的性质和等量代换可证明∠2+∠6=180°,最后依据平行线的判定定理和平行公理的推论进行证明即可.
解答 解:因为∠1+∠2=180°,∠2+∠4=180°(已知),
所以∠1=∠4,(同角的补角相等)
所以a∥c.(内错角相等,两直线平行)
又因为∠2+∠3=180°(已知)
∠3=∠6(对顶角相等)
所以∠2+∠6=180°,(等量代换)
所以a∥b.(同旁内角互补,两直线平行)
所以b∥c.(平行与同一条直线的两条直线平行).
故答案为:同角的补角相等;内错角相等,两直线平行;对顶角相等;等量代换;同旁内角互补,两直线平行;平行与同一条直线的两条直线平行.
点评 本题主要考查的是平行线的判定,熟练掌握平行线的判定定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.若(x+p)(x+2)=x2+2p,则p的值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
19.如果∠1与∠2互为补角,∠1>∠2,那么∠2的余角等于( )
| A. | $\frac{1}{2}$(∠1+∠2) | B. | $\frac{1}{2}$∠1 | C. | $\frac{1}{2}$(∠1-∠2) | D. | ∠1-∠2 |
9.若m=$\sqrt{40}$-2,则估计m的值所在的范围是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |
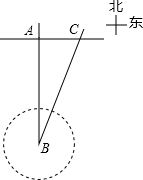 台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问:
台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问: 将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.
将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.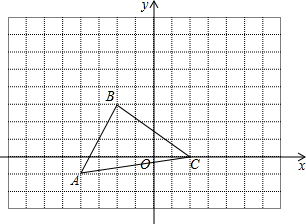 如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1.
如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1.