题目内容
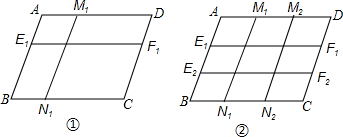
(1)如图①,在?ABCD中,E1F1∥AD,M1N1∥AB,那么图中共有 个平行四边形.
(2)如图②,在?ABCD中.E2F2∥AD,M2N2∥AB,那么图中共有 个平行四边形.
(3)一般地,在?ABCD中,如果有E1F1∥AD,E2F2∥AD,…,EnFn∥AD,M1N1∥AB,M2N2∥AB,…,MnNn∥AB,你能猜测出图中共有多少个平行四边形吗?说说你的理由.
(2)如图②,在?ABCD中.E2F2∥AD,M2N2∥AB,那么图中共有
(3)一般地,在?ABCD中,如果有E1F1∥AD,E2F2∥AD,…,EnFn∥AD,M1N1∥AB,M2N2∥AB,…,MnNn∥AB,你能猜测出图中共有多少个平行四边形吗?说说你的理由.

考点:平行四边形的判定与性质
专题:
分析:(1)由在平行四边形ABCD中,EF∥AB,GH∥AD,易得平行四边形有:?ABCD,?ABFE,?EFCD,?AGHD,?BCHG,?OEDH,?OFCH,?OEAG,?OGBF共9个,得出规律;
(2)根据规律得出有6×6=36个平行四边形;
(3)根据规律得出有
×
=
个平行四边形.
(2)根据规律得出有6×6=36个平行四边形;
(3)根据规律得出有
| (n+1)(n+2) |
| 2 |
| (n+1)(n+2) |
| 2 |
| (n+1)2(n+2)2 |
| 4 |
解答:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
综上所述:图①中:AD边上有:AM1、AD、M1D三条线段;
AB边上有:AE1,AB,E1B三条线段,
故共有3×3=9个平行四边形;
故答案为:9;
(2)由(1)得:图②中,AD边上有:AM1、AM2、AD、M1M2、M1D、M2D六条线段,
AB边上有:AE1、AE2、AB、E1E2、E1B、E2B六条线段,
故共有6×6=36个平行四边形;
故答案为:36;
(3)
个平行四边形;理由如下:
一般地,若有E1F1∥E2F2∥E3F3∥…∥EnFn∥AD时;则AB边上有:1+2+3+..+n+(n+1)=
条线段,
同理,若有M1N1∥M2N2∥M3N3∥…∥MnNn∥AB时;则AD边上有:1+2+3+..+n+(n+1)=
条线段,
则共有
×
=
个平行四边形.
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
综上所述:图①中:AD边上有:AM1、AD、M1D三条线段;
AB边上有:AE1,AB,E1B三条线段,
故共有3×3=9个平行四边形;
故答案为:9;
(2)由(1)得:图②中,AD边上有:AM1、AM2、AD、M1M2、M1D、M2D六条线段,
AB边上有:AE1、AE2、AB、E1E2、E1B、E2B六条线段,
故共有6×6=36个平行四边形;
故答案为:36;
(3)
| (n+1)2(n+2)2 |
| 4 |
一般地,若有E1F1∥E2F2∥E3F3∥…∥EnFn∥AD时;则AB边上有:1+2+3+..+n+(n+1)=
| (n+1)(n+2) |
| 2 |
同理,若有M1N1∥M2N2∥M3N3∥…∥MnNn∥AB时;则AD边上有:1+2+3+..+n+(n+1)=
| (n+1)(n+2) |
| 2 |
则共有
| (n+1)(n+2) |
| 2 |
| (n+1)(n+2) |
| 2 |
| (n+1)2(n+2)2 |
| 4 |
点评:本题考查了平行四边形的判定与性质;根据题意找出规律是解决问题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 实数a在数轴上的位置如图所示,则
实数a在数轴上的位置如图所示,则| (a-3)2 |
| (a-9)2 |
| A、6 | B、-6 |
| C、2a-12 | D、无法确定 |
 如图,在△ABC中,∠B=45°,∠A=105°,AC=2,求BC的长.
如图,在△ABC中,∠B=45°,∠A=105°,AC=2,求BC的长. 如图,在Rt△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经过多长时间,△PBQ的面积等于6cm2?
如图,在Rt△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经过多长时间,△PBQ的面积等于6cm2? 如图,正方形ABCD的周长为8cm,顺次连接正方形ABCD各边的中点,得到正方形EFGH,则四边形EFGH的周长等于
如图,正方形ABCD的周长为8cm,顺次连接正方形ABCD各边的中点,得到正方形EFGH,则四边形EFGH的周长等于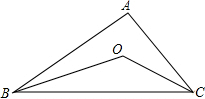 如图所示,BO,CO分别平分∠ABC和∠ACB.
如图所示,BO,CO分别平分∠ABC和∠ACB.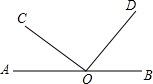 如图,∠AOC和∠BOD
如图,∠AOC和∠BOD