题目内容
 如图,正方形ABCD的周长为8cm,顺次连接正方形ABCD各边的中点,得到正方形EFGH,则四边形EFGH的周长等于
如图,正方形ABCD的周长为8cm,顺次连接正方形ABCD各边的中点,得到正方形EFGH,则四边形EFGH的周长等于考点:中点四边形
专题:
分析:由条件可求得正方形ABCD的边长,在Rt△AEH中可求得EH,则可求得答案.
解答:解:∵四边形ABCD为正方形,
∴AB=BC=CD=DA,∠A=90°,
∵正方形ABCD的周长为8cm,
∴AB=AD=2cm,
又∵E、H为AB、AD的中点,
∴AE=EH=
AB=1cm,
在Rt△AEH中,由勾股定理可求得EH=
cm,
∴正方形EFGH的周长为4EH=4
cm,正方形EFGH的面积为EH2=(
)2=2cm2.
故答案为:4
;2.
∴AB=BC=CD=DA,∠A=90°,
∵正方形ABCD的周长为8cm,
∴AB=AD=2cm,
又∵E、H为AB、AD的中点,
∴AE=EH=
| 1 |
| 2 |
在Rt△AEH中,由勾股定理可求得EH=
| 2 |
∴正方形EFGH的周长为4EH=4
| 2 |
| 2 |
故答案为:4
| 2 |
点评:本题主要考查正方形的性质,掌握正方形的四边相等且每个角都为直角是解题的关键.

练习册系列答案
相关题目
 实数a,b在数轴上的对应点如图所示,则
实数a,b在数轴上的对应点如图所示,则| a2b2 |
| A、-ab | B、ab |
| C、±ab | D、|a|b |
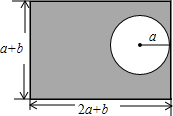 某个居民小区的长方形花园的长、宽分别为2a+b和a+b,中间有一个半径为a的圆形游乐场(如图),请你用代数式表示图中阴影部分的面积,再求当a=5米,b=10米时阴影部分面积(π取3.14).
某个居民小区的长方形花园的长、宽分别为2a+b和a+b,中间有一个半径为a的圆形游乐场(如图),请你用代数式表示图中阴影部分的面积,再求当a=5米,b=10米时阴影部分面积(π取3.14). 如图,二次函数y=x2+m的图形与直线y=2x相交于 A、B两点,且C为顶点.若OA:OB=1:2,求m的值.
如图,二次函数y=x2+m的图形与直线y=2x相交于 A、B两点,且C为顶点.若OA:OB=1:2,求m的值.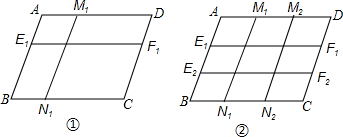
 如图所示,某人到岛上去探宝,从A处登陆后先往东走8km,又往北走1.5km,遇到障碍后又往西走2.5km,再折回向北走到6.5km处往东一拐,仅走0.5km就找到了宝藏,问登陆点A与宝藏埋藏点B之间的距离是多少?
如图所示,某人到岛上去探宝,从A处登陆后先往东走8km,又往北走1.5km,遇到障碍后又往西走2.5km,再折回向北走到6.5km处往东一拐,仅走0.5km就找到了宝藏,问登陆点A与宝藏埋藏点B之间的距离是多少?
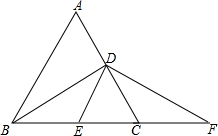 如图,在△ABC中,AB=AC,∠A=60°,BD⊥AC于点D,E为BC的中点,DF⊥DE,交BC的延长线于点F,求证:E,C两点是线段BF的等分点.
如图,在△ABC中,AB=AC,∠A=60°,BD⊥AC于点D,E为BC的中点,DF⊥DE,交BC的延长线于点F,求证:E,C两点是线段BF的等分点.