题目内容
请你写出一个图象开口向上，且经过（0，1）的二次函数的表达式 ．
考点：二次函数的性质
专题：开放型
分析：设二次函数的表达式为y=ax2+bx+c（a≠0），根据a＞0时开口向上，可取a=1，将（0，1）代入得出c=1，即可得出二次函数表达式．
解答：解：设二次函数的表达式为y=ax2+bx+c（a≠0），
∵图象为开口向上，且经过（0，1），
∴a＞0，c=1，
∴二次函数表达式可以为：y=x2+1（答案不唯一）．
故答案为：y=x2+1（答案不唯一）．
∵图象为开口向上，且经过（0，1），
∴a＞0，c=1，
∴二次函数表达式可以为：y=x2+1（答案不唯一）．
故答案为：y=x2+1（答案不唯一）．
点评：此题主要考查了二次函数的性质，得出a的符号和c=1是解题关键．
练习册系列答案
相关题目
甲乙两地相距150千米，一辆小汽车和一辆客车同时从两地相向开出，经过50分钟相遇，此时小汽车比客车多行驶30千米．设小汽车和客车的平均速度分别为x千米/小时和y千米/小时．则下列方程组正确的是（ ）
A、
| |||||||||||||
B、
| |||||||||||||
C、
| |||||||||||||
D、
|
如图，已知点A（0，4），B（2，0），点M是线段AB上一动点（不与点、B重合），以M为顶点的抛物线y=（x-m）2+n与直线OA交于点C，求线段AC长度的取值范围．当x≠-
时，
=2成立，则a2-b2等于（ ）
| 5 |
| b |
| a+x |
| -bx-5 |
| A、0 | B、1 |
| C、99.25 | D、99.75 |
如图，二次函数y=x2+m的图形与直线y=2x相交于 A、B两点，且C为顶点．若OA：OB=1：2，求m的值．
如图，在Rt△ABC中，∠C=90°，AC=12cm，BC=6cm，点P从点C开始沿CB向点B以1cm/s的速度移动，点Q从A开始沿AC向点C以2cm/s的速度移动，如果点P，Q同时从点C，A出发，试问：
如图所示，某人到岛上去探宝，从A处登陆后先往东走8km，又往北走1.5km，遇到障碍后又往西走2.5km，再折回向北走到6.5km处往东一拐，仅走0.5km就找到了宝藏，问登陆点A与宝藏埋藏点B之间的距离是多少？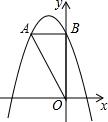
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连结OA．