题目内容
实数a在数轴上的位置如图所示，则| (a-3)2 |
| (a-9)2 |
| A、6 | B、-6 |
| C、2a-12 | D、无法确定 |
考点：实数与数轴,二次根式的性质与化简
专题：
分析：先根据各点在数轴上的位置判断出a-3及a-9的符号，再根据二次根式的性质把原式进行化简即可．
解答：解：∵由图可知4＜a＜8，
∴a-3＞0，a-9＜0，
∴原式=a-3+9-a=6．
故选A．
∴a-3＞0，a-9＜0，
∴原式=a-3+9-a=6．
故选A．
点评：本题考查的是实数与数轴，熟知实数与数轴上各点是一一对应关系是解答此题的关键．
练习册系列答案
相关题目
如图，下列推论及所注理由正确的是（ ）| A、∵∠1=∠B，∴DE∥BC（两直线平行，同位角相等） |
| B、∵∠2=∠C，∴DE∥BC（两直线平行，同位角相等） |
| C、∵∠2+∠3+∠B=180°，∴DE∥BC（同旁内角互补，两直线平行） |
| D、∵∠4=∠1，∴DE∥BC（对顶角相等） |
当x≠-
时，
=2成立，则a2-b2等于（ ）
| 5 |
| b |
| a+x |
| -bx-5 |
| A、0 | B、1 |
| C、99.25 | D、99.75 |
如图，在Rt△ABC中，∠C=90°，AC=12cm，BC=6cm，点P从点C开始沿CB向点B以1cm/s的速度移动，点Q从A开始沿AC向点C以2cm/s的速度移动，如果点P，Q同时从点C，A出发，试问：
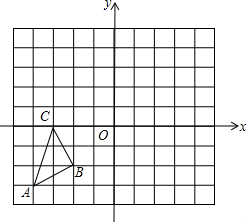如图，在边长为1个单位长度的小正方形组成的网格中，O为坐标原点，A（-4，-3），B（-2，-2），C（-3，0）．
如图所示，某人到岛上去探宝，从A处登陆后先往东走8km，又往北走1.5km，遇到障碍后又往西走2.5km，再折回向北走到6.5km处往东一拐，仅走0.5km就找到了宝藏，问登陆点A与宝藏埋藏点B之间的距离是多少？
阅读下列内容：
如图，AB⊥CD，垂足为O，EF经过点O，∠2=2∠1，求∠2，∠3，∠BOE的度数．