题目内容
5.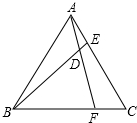 已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.
已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.(1)说明△ABE≌△CAF;
(2)求∠BDF的度数.
分析 (1)根据等边三角形的性质可得,∠BAC=∠C=60°,AB=CA,然后利用“边角边”证明△ABE和△CAF全等;
(2)根据全等三角形对应角相等可得∠ABE=∠CAF,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式整理得到∠ADE=∠BAC.
解答 (1)证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=CA,
即∠BAE=∠C=60°,
在△ABE和△CAF中,
$\left\{\begin{array}{l}{AB=CA}\\{∠BAC=∠C}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CAF(SAS);
(2)解:∵△ABE≌△CAF,
∴∠ABE=∠CAF,
∴∠ADE=∠ABE+∠BAF=∠CAF+∠BAF=∠BAC=60°.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质等边三角形的性质得到三角形全等是条件是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
15.化简:$\sqrt{(1-sin52°)^{2}}$-$\sqrt{(1-tan52°)^{2}}$的结果是( )
| A. | tan52°-sin52° | B. | sin52°-tan52° | C. | 2-sin52°-tan52° | D. | -sin52°-tan52° |
 如图,AB=AD,DC=BC,∠B与∠D相等吗?为什么?
如图,AB=AD,DC=BC,∠B与∠D相等吗?为什么?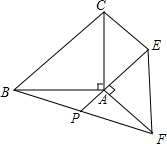 如图,等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,连结CE、BF,延长EA交BF于P,当点P为BF的中点时,求$\frac{CE}{AP}$的值.
如图,等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,连结CE、BF,延长EA交BF于P,当点P为BF的中点时,求$\frac{CE}{AP}$的值.