题目内容
8.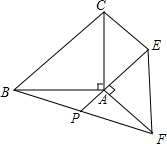 如图,等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,连结CE、BF,延长EA交BF于P,当点P为BF的中点时,求$\frac{CE}{AP}$的值.
如图,等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,连结CE、BF,延长EA交BF于P,当点P为BF的中点时,求$\frac{CE}{AP}$的值.
分析 延长FA到G使AG=AF,如图,易得PA为△FBG的中位线,则BG=2PA,再根据等腰直角三角形的性质得AB=AC,AE=AF,∠GAE=90°,则AG=AE,接着证明△ABG≌△ACE,得到BG=CE,所以CE=2PA,于是可得到$\frac{CE}{AP}$的值.
解答 解:延长FA到G使AG=AF,如图,
∵点P为BF的中点,
∴PA为△FBG的中位线,
∴BG=2PA,
∵等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,
∴AB=AC,AE=AF,∠GAE=90°,
∴AG=AE,
∵∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△ABG和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠2=∠1}\\{AG=AE}\end{array}\right.$,
∴△ABG≌△ACE,
∴BG=CE,
∴CE=2PA,
∴$\frac{CE}{AP}$=2.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.解决本题的关键是构建△ABG与△ACE全等.

练习册系列答案
相关题目
6. 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )| A. | 0<x<1 | B. | -1<x<0 | C. | x<0或x>1 | D. | x<-1或x>0 |
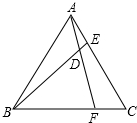 已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.
已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.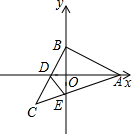 如图,在直角坐标系中,点A(8,0),点B(0,4),点C(-4,-4),连接BC与x轴相交于点D,连接AC与y轴相交于点E,连接DE.
如图,在直角坐标系中,点A(8,0),点B(0,4),点C(-4,-4),连接BC与x轴相交于点D,连接AC与y轴相交于点E,连接DE.
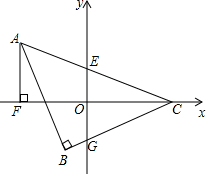 如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.
如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.