题目内容
15.化简:$\sqrt{(1-sin52°)^{2}}$-$\sqrt{(1-tan52°)^{2}}$的结果是( )| A. | tan52°-sin52° | B. | sin52°-tan52° | C. | 2-sin52°-tan52° | D. | -sin52°-tan52° |
分析 根据正弦、正切的增减性比较1与sin52°、1与tan52°的大小,根据二次根式的性质化简合并即可.
解答 解:∵1-sin52°>0,1-tan52°<0,
∴$\sqrt{(1-sin52°)^{2}}$-$\sqrt{(1-tan52°)^{2}}$=1-sin52°-tan52°+1=2-sin52°-tan52°.
故选:C.
点评 本题考查的是二次根式的化简,掌握二次根式的性质和正弦、正切的增减性是解题的关键.

练习册系列答案
相关题目
4.袋中装有大小一样的白球和黑球各3个,从中任取2个球,则两个均为黑球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
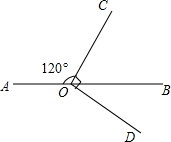 如图,已知∠AOC=120°,∠COD是直角,∠BOC=2∠BOD.问点A、O、B在一条直线上吗?为什么?
如图,已知∠AOC=120°,∠COD是直角,∠BOC=2∠BOD.问点A、O、B在一条直线上吗?为什么?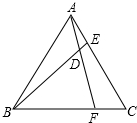 已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.
已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.