题目内容
5.某商店如果将进货价格为8元的商品按每件10元售出,每天可销售2000件,现采取提高售价,减少进货量的方法,增加利润,已知这种商品每涨价0.5元,其销售量就减少100件,问应将售价定为多少元时可赚利润6400元?这时应进货多少个?分析 根据等量关系“利润=(售价-进价)×销量”列出方程即可求解.
解答 解:设每件售价定为x元时,才能使每天利润为6400元,
(x-8)[2000-200(x-10)]=6400,
解得:x1=12,x2=16,
∵采取提高售价,减少进货量的方法,增加利润,
∴x取16.
答:应将每件售价定为16元时,能使每天利润为6400元.
点评 此题主要考查了一元二次方程的应用,解题的关键是了解利润与销量及单价之间的关系,同学们应重点掌握.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
15. 如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
 如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )
如图,已知∠AOC=α,OA⊥OB,OC⊥OD,则∠BOD=( )| A. | 180°-α | B. | 90°-α | C. | 90°+$\frac{1}{2}$α | D. | 2α-90° |
10.若|2a|=-2a,则a一定是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
 如图,AC:BC=5:7,AD:BD=5:11,若CD=11cm,则AB=$\frac{528}{5}$cm.
如图,AC:BC=5:7,AD:BD=5:11,若CD=11cm,则AB=$\frac{528}{5}$cm.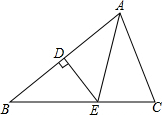 已知,如图,∠ABC中,AB=BC,DE是AB的中垂线,且BE=AC,求证:∠B=∠EAC.
已知,如图,∠ABC中,AB=BC,DE是AB的中垂线,且BE=AC,求证:∠B=∠EAC.