题目内容
13.已知一元二次方程ax2-4x+1=0有两个不相等的实数根,求a的取值范围.分析 根据根的判别式建立关于a的不等式,注意a的数值不能为0,由此两者结合得出答案即可.
解答 解:∵关于x的一元二次方程ax2-4x+1=0有两个不相等的实数根,
∴a≠0且△>0,即(-4)2-4•a•1>0,解得a<4,
∴a的取值范围为a<4且a≠0.
∴当a<4且a≠0时,关于x的一元二次方程ax2-4x+1=0有两个不相等的实数根.
点评 本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
3.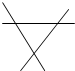 如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )
如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )
 如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )
如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )| A. | 4处 | B. | 3处 | C. | 2处 | D. | 1处 |
18. 如图,∠A=60°,∠B=80°,则∠1+∠2=( )
如图,∠A=60°,∠B=80°,则∠1+∠2=( )
 如图,∠A=60°,∠B=80°,则∠1+∠2=( )
如图,∠A=60°,∠B=80°,则∠1+∠2=( )| A. | 100° | B. | 120° | C. | 140° | D. | 150° |
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有4个.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有4个.