题目内容
3．证明：直角三角形的两个锐角互余．分析 作出图形，写出已知、求证，然后根据三角形的内角和等于180°列方程整理即可得证．
解答 
已知：如图，在△ABC中，∠C=90°，
求证：∠A+∠B=90°，
证明：∵在△ABC中，∠A+∠B+∠C=180°，
又∵∠C=90°，
∴∠A+∠B=180°-∠C=180°-90°=90°．
点评 本题考查了直角三角形两锐角互余的性质的证明，比较简单，要掌握此类文字叙述性命题的证明格式．
练习册系列答案
相关题目
14．
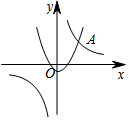如图，抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1，则关于x的不等式$\frac{k}{x}$+x2+m＜0的解集是（ ）
如图，抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1，则关于x的不等式$\frac{k}{x}$+x2+m＜0的解集是（ ）| A． | x＞1 | B． | x＜-1 | C． | 0＜x＜1 | D． | -1＜x＜0 |
18．下列计算正确的是（ ）
| A． | a2•a3=a6 | B． | （x3）3=x6 | C． | a6÷a=a6 | D． | x5+x5=2x5 |
8．
如图，反比例函数y=$\frac{k}{x}$（x＜0）的图象经过点P，若矩形的面积是6，则k的值为（ ）
如图，反比例函数y=$\frac{k}{x}$（x＜0）的图象经过点P，若矩形的面积是6，则k的值为（ ）| A． | -6 | B． | -5 | C． | 6 | D． | 5 |
15．一次函数y=-$\frac{4}{3}$x+1的图象与两坐标轴所围成的三角形的面积为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{3}{8}$ | C． | $\frac{4}{3}$ | D． | $\frac{8}{3}$ |
