题目内容
6.在Rt△ABC中,斜边AB=5厘米,BC=a厘米,AC=b厘米,a>b,且a、b是方程x2-(m-1)x+m+4=0的两根,Rt△ABC的面积为6平方厘米.分析 根据勾股定理求的a2+b2=25,即a2+b2=(a+b)2-2ab①,然后根据根与系数的关系求的a+b=m-1②ab=m+4③;最后由①②③联立方程组,即可求得m的值,继而可得答案.
解答 解:∵斜边AB为5的Rt△ABC中,∠C=90°,两条直角边a、b,
∴a2+b2=25,
又∵a2+b2=(a+b)2-2ab,
∴(a+b)2-2ab=25,①
∵a、b是关于x的方程x2-(m-1)x+m+4=0的两个实数根,
∴a+b=m-1,②
ab=m+4,③
由①②③,解得
m=-4,或m=8;
当m=-4时,ab=0,
∴a=0或b=0,(不合题意)
∴m=8;
则Rt△ABC的面积为$\frac{1}{2}$ab=$\frac{1}{2}$×(8+4)=6,
故答案为:6.
点评 本题综合考查了根与系数的关系、勾股定理的应用.解答此题时,需注意作为三角形的两边a、b均不为零这一条件.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | |a|一定是正数 | |
| B. | 在同一平面内,过直线外或直线上一点,有且只有一条直线垂直于已知直线 | |
| C. | 两个无理数的和仍是无理数 | |
| D. | 如果两个角互补,那么一个是锐角,一个是钝角 |
11.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列方程中,是二元一次方程的是( )
| A. | x2+y2=5 | B. | $\frac{1}{x}$+$\frac{1}{y}$=2 | C. | x+y+z=3 | D. | $\frac{x}{2}$-$\frac{y}{3}$=$\frac{1}{4}$ |
 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知AD=10cm,BF=6cm,求图中阴影部分的面积.
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知AD=10cm,BF=6cm,求图中阴影部分的面积.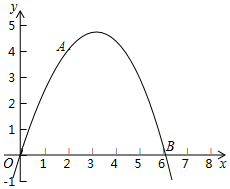 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
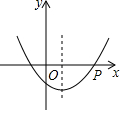 如图,抛物线y=ax2+bx+c的对称轴是经过点(1,0)且平行于y轴的直线,若点P(4,0)在抛物线上,则4a-2b+c的值为( )
如图,抛物线y=ax2+bx+c的对称轴是经过点(1,0)且平行于y轴的直线,若点P(4,0)在抛物线上,则4a-2b+c的值为( )