题目内容
17.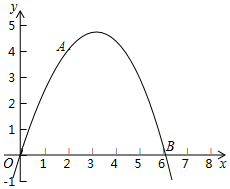 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).(1)求a,b的值;
(2)若点C是该二次函数的最高点,求△OBC的面积.
分析 (1)利用待定系数法确定a、b的值即可;
(2)确定其顶点坐标后即可求得三角形OBC的面积.
解答 解:(1)将点A(2,4)与B(6,0)代入y=ax2+bx,
得:$\left\{\begin{array}{l}{4a+2b=4}\\{36a+6b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=3}\end{array}\right.$;
(2)由(1)知,y=-$\frac{1}{2}$x2+3x=-$\frac{1}{2}$(x-3)2+$\frac{9}{2}$,
∴点C的坐标为(3,$\frac{9}{2}$),
∴S△OBC=$\frac{1}{2}$×6×$\frac{9}{2}$=$\frac{27}{2}$.
点评 本题主要考查待定系数法和二次函数的最值,熟练掌握待定系数法求函数解析式及二次函数的顶点式求函数的最值是解题的关键.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
8.以下列各组数作为三角形的三边长,其中不能构成直角三角形的是( )
| A. | 1,1,$\sqrt{2}$ | B. | 6,8,10 | C. | 8,15,17 | D. | 1,2,2 |
14.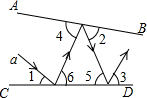 光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=25°,∠3=75°,则∠2=( )
光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=25°,∠3=75°,则∠2=( )
 光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=25°,∠3=75°,则∠2=( )
光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=25°,∠3=75°,则∠2=( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
 如图,∠1=∠2=45°,∠3=75°,则∠4=105°.
如图,∠1=∠2=45°,∠3=75°,则∠4=105°.
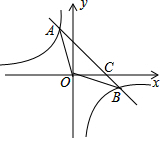 如图,一次函数y=-x+2的图象与反比例函数的图象y=$\frac{k}{x}$交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y=-x+2的图象与反比例函数的图象y=$\frac{k}{x}$交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.