题目内容
5.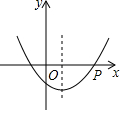 如图,抛物线y=ax2+bx+c的对称轴是经过点(1,0)且平行于y轴的直线,若点P(4,0)在抛物线上,则4a-2b+c的值为( )
如图,抛物线y=ax2+bx+c的对称轴是经过点(1,0)且平行于y轴的直线,若点P(4,0)在抛物线上,则4a-2b+c的值为( )| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
分析 根据对称性确定抛物线与x轴的另一交点为(-2,0),代入解析式即可.
解答 解:由题意得:抛物线的对称轴是:直线x=1,
∵点P(4,0)在抛物线上,
∴抛物线与x轴另一交点坐标为(-2,0),
即当x=-2时,y=0,
4a-2b+c=0,
故选B.
点评 本题考查了抛物线与x轴的交点问题,常利用对称性确定对称轴或抛物线与x轴的交点坐标,明确抛物线与x轴的两交点到对称轴与x轴的交点的距离相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.以下列各组数作为三角形的三边长,其中不能构成直角三角形的是( )
| A. | 1,1,$\sqrt{2}$ | B. | 6,8,10 | C. | 8,15,17 | D. | 1,2,2 |
10.关于x的一元二次方程x2-3x-k2=0(k是常数)的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 方程根的情况与k的取值有关 |
17.在$\sqrt{2}$,-$\sqrt{3}$,1,0这四个数中,最小的一个数是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | 0 |
14.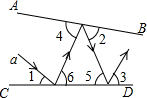 光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=25°,∠3=75°,则∠2=( )
光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=25°,∠3=75°,则∠2=( )
 光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=25°,∠3=75°,则∠2=( )
光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=25°,∠3=75°,则∠2=( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
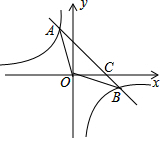 如图,一次函数y=-x+2的图象与反比例函数的图象y=$\frac{k}{x}$交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y=-x+2的图象与反比例函数的图象y=$\frac{k}{x}$交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.