题目内容
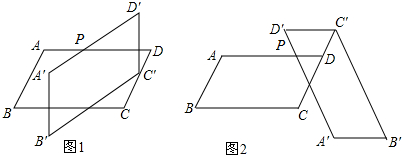
1.在?ABCD中,∠ABC=60°,AB=4,BC=8,将?ABCD绕AD边上任意一点P逆时针旋转(点P不与A、D重合),得到?A′B′C′D′,且点C′落在CD(或其延长线上),如图所示.(1)如图1,当旋转角为30°时,求PD的长.
(2)当旋转角度数为n(0°<n<120°)时,PD=$\frac{2\sqrt{3}}{tan(30°+\frac{1}{2}n)}$+2(用含n的式子表示).
分析 (1)如图1中,连接PC、PC′作PN⊥CD于N,CM⊥AD于M,首先证明∠CPM=45°推出CM=PM,求出PM,DM即可解决问题.
(2)分两种情形①如图1中,当C′在CD上时,②如图2中,当点C′在线段CD的延长线时,连接PC、PC′作PN⊥CD于N,CM⊥AD于M,分别在RT△PCM,RT△CMD中解三角形即可解决问题.
解答 解:(1)如图1中,连接PC、PC′作PN⊥CD于N,CM⊥AD于M,
∵PC=PC′,∠CPC′=30°,
∴∠PC′C=∠PCC′=75°,
∵∠PC′C=∠PDC+∠DPC′,∠B=∠D=60°,
∴∠DPC′=15°,
∴∠CPM=45°,
∵∠CMP=90°,
∴∠CPM=∠PCM=45°,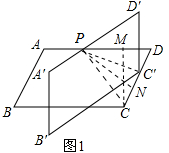
∴PM=CM,
在RT△CMD中,∵∠CMD=90°,CD=4,∠D=60°,
∴DM=$\frac{1}{2}$CD=2,CM=PM=2$\sqrt{3}$,
∴PD=2+2$\sqrt{3}$,
(2)①如图1中,当C′在CD上时,由(1)可知,∠CPC′=n,则∠PC′C=90°-$\frac{1}{2}$n,
∠DPC′=90°-$\frac{1}{2}$n-60°=30°-$\frac{1}{2}$n,∠CPM=30°-$\frac{1}{2}$n+n=30°+$\frac{1}{2}$n,
∴PD=PM+DM=$\frac{2\sqrt{3}}{tan(30°+\frac{1}{2}n)}$+2.
②如图2中,当点C′在线段CD的延长线时,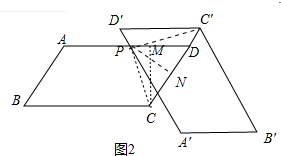 连接PC、PC′作PN⊥CD于N,CM⊥AD于M,
连接PC、PC′作PN⊥CD于N,CM⊥AD于M,
同理可得∠CPM=30°+$\frac{1}{2}$n,
∵0<n<120°,
∴∠CPM<90°,
PD=PM+DM=$\frac{2\sqrt{3}}{tan(30°+\frac{1}{2}n)}$+2,
综上所述PD=$\frac{2\sqrt{3}}{tan(30°+\frac{1}{2}n)}$+2.
故答案为$\frac{2\sqrt{3}}{tan(30°+\frac{1}{2}n)}$+2.
点评 不通考查旋转变换、平行四边形的性质,直角三角形中30度角所对的直角边等于斜边的一半、锐角三角函数等知识,解题的关键是学会添加常用辅助线,把问题转化为解直角三角形问题,属于中考常考题型.

| A. | $\frac{by}{2ay}=\frac{b}{2a}$ | B. | $-\frac{y}{x}=\frac{-y}{-x}$ | ||
| C. | 1+$\frac{1}{a}$=$\frac{2}{a}$ | D. | $\frac{{{a^2}+ab}}{{{b^2}+ab}}=\frac{a^2}{b^2}$ |
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | C. | -$\sqrt{(-3)^{2}}$=3 | D. | $\sqrt{2}$•$\sqrt{5}$=$\sqrt{10}$ |
 如图所示,点C是线段AB上一点,AC<CB,M、N分别是AB、CB的中点,AC=8,NB=5,则线段MN=4.
如图所示,点C是线段AB上一点,AC<CB,M、N分别是AB、CB的中点,AC=8,NB=5,则线段MN=4. 直线AB,CD相交于点O,OE平分∠AOD,∠COF=90°,∠BOF=40°,求∠AOC与∠AOE的度数.
直线AB,CD相交于点O,OE平分∠AOD,∠COF=90°,∠BOF=40°,求∠AOC与∠AOE的度数.