题目内容
6．方程3x+2y-7=0经变形后得y=-$\frac{3}{2}$x+$\frac{7}{2}$．．分析 将x看做已知数求出y即可．
解答 解：方程3x+2y-7=0，
解得：y=-$\frac{3}{2}$x+$\frac{7}{2}$．
故答案为：-$\frac{3}{2}$x+$\frac{7}{2}$．
点评 此题考查了解二元一次方程，解题的关键是将x看做已知数求出y．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．
已知实数a在数轴上的位置如图所示，则化简|a-1|+$\sqrt{{a}^{2}}$的结果是（ ）
已知实数a在数轴上的位置如图所示，则化简|a-1|+$\sqrt{{a}^{2}}$的结果是（ ）| A． | -1 | B． | 1 | C． | 1-2a | D． | 2a-1 |
5．如图所示的是四个物理实验工具的简图，从左到右依次是小车、弹簧、钩码、三极管，其中是轴对称图形的是（ ）
| A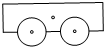． |  小车 | B． |  弹簧 | C． |  钩码 | D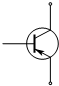． |  三极管 |
如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=5cm，求EF的长．
18．已知$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$且0＜y-x＜1，则k的取值范围是（ ）
| A． | -1$＜k＜-\frac{1}{2}$ | B． | 0$＜k＜\frac{1}{2}$ | C． | 0＜k＜1 | D． | $\frac{1}{2}$＜k＜1 |
16．在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出下列定义：若b′=$\left\{\begin{array}{l}{b，}&{a≥1}\\{-b，}&{a＜1}\end{array}\right.$，则称点Q为点的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（-2，5）的限变点的坐标是（-2，-5），如果一个点的限变点的坐标是（$\sqrt{3}$，-1），那么这个点的坐标是（ ）
| A． | （-1，$\sqrt{3}$） | B． | （-$\sqrt{3}$，-1） | C． | （$\sqrt{3}$，-1） | D． | （$\sqrt{3}$，1） |