题目内容
6.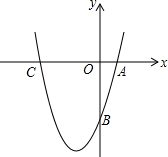 如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.(1)求抛物线的解析式;
(2)求抛物线的顶点坐标,对称轴,点C的坐标;
(3)根据图象,写出y>0时,x的取值范围;
(4)求△ABC面积;
(5)⊙P的半径为2,圆心P在此抛物线上运动,当⊙P与y轴相切时,求圆心P的坐标.
分析 (1)将A、B两点坐标代入即可求出;
(2)将抛物线解析式配成顶点式即可知道顶点坐标和对称轴,配成交点式即可知道C点坐标;
(3)y>0表示抛物线的图象高于x轴的部分,由图象可直接写出对应的x的取值范;
(4)求出AC、OB即可;
(5)圆与y轴相切,说明圆心到y轴的距离等于半径,圆心到y轴的距离就是P点的横坐标的绝对值;
解答 解:(1)∵抛物线y=x2+bx-3a过点A(1,0),B(0,-3),
∴$\left\{\begin{array}{l}{1+b-3a=0}\\{-3a=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,
∴抛物线的解析式为:y=x2+2x-3;
(2)∵y=x2+2x-3=(x+1)2-4=(x+3)(x-1),
∴抛物线的顶点坐标为(-1,-4),对称轴为x=-1,C(-3,0);
(3)由图象可知:y>0时,x<-3或x>1;
(4)∵A(1,0),C(-3,0),
∴AC=4,
∵OB=3,
∴${S}_{△ABC}=\frac{1}{2}×4×3$=6;
(5)设点P的横坐标为,则|x|=2,
当x=-2时,y=-3,
∴P(-2,-3);
当x=2时,y=5,
∴P(2,5);
综上所述,圆心P的坐标可以为:(-2,-3)、(2,5).
点评 本题考查了待定系数法求二次函数解析式、二次函数的顶点式、二次函数的交点式、二次函数的图象性质、三角形面积求法、圆与直线相切的性质等知识点,难度不大.纵观本题五个小问,全部着重考查同学们对基础知识的掌握情况,这就要求同学们对每一个概念、定理、公式、基本结论都要理解透彻,掌握牢固.

练习册系列答案
相关题目
15.如果a与-$\sqrt{5}$互为相反数,则a的值是( )
| A. | 5 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | ±$\sqrt{5}$ |
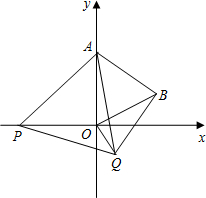 如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记点Q的位置为B,则当点P从(-2,0)运动到(2,0)时,点Q运动的路径长为4.
如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记点Q的位置为B,则当点P从(-2,0)运动到(2,0)时,点Q运动的路径长为4.
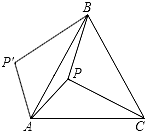 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$.
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$.