题目内容
10．已知关于x的一元二次方程x2+（k-1）x+k2=0两根的积为1，求k的值．分析 由关于x的一元二次方程x2+（k-1）x+k2=0两根的积为1，可得k2=1且△≥0，继而求得答案．
解答 解：∵关于x的一元二次方程x2+（k-1）x+k2=0两根的积为1，
∴k2=1，
解得：k=±1，
∵△=（k-1）2-4k2=-3k2-2k+1≥0，
∴k=-1．
点评 此题考查了根与系数的关系以及根的判别式．注意若x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q．
练习册系列答案
出彩同步大试卷系列答案
相关题目
2．设两组数a1，a2，a3，…，an和b1，b2，b3，…，bn的平均数分别为$\overline{a}$和$\overline{b}$，那么新的一组数a1+b1，a2+b2，a3+b3，…an+bn的平均数是（ ）
| A． | $\frac{1}{2}（\overline{a}+\overline{b}）$ | B． | $\overline{a}+\overline{b}$ | C． | $\frac{1}{n}（\overline{a}+\overline{b}）$ | D． | 以上都不对 |
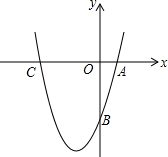如图，已知抛物线y=x2+bx-3a过点A（1，0），B（0，-3），与x轴交于另一点C．