题目内容
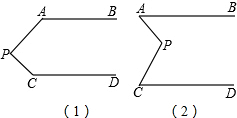 如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.
如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.结论:(1)
(2)
选择结论
考点:平行线的性质
专题:
分析:(1)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,同旁内角互补,即可求得∠PAB+∠1=180°,∠2+∠PCD=180°,则可得∠APC+∠PAB+∠PCD=∠PBA+∠1+∠2+∠PCD=360°;
(2)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠PAB,∠2=∠PCD,则可得∠APC=∠PAB+∠PCD.
(2)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠PAB,∠2=∠PCD,则可得∠APC=∠PAB+∠PCD.
解答: 解:(1)∠APC+∠PAB+∠PCD=360°.理由如下:
解:(1)∠APC+∠PAB+∠PCD=360°.理由如下:
过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,
∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD.理由如下:
过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,
∴∠APC=∠PAB+∠PCD.
故答案为:∠APC+∠PAB+∠PCD=360°;∠APC=∠PAB+∠PCD;∠APC+∠PAB+∠PCD=360°.
 解:(1)∠APC+∠PAB+∠PCD=360°.理由如下:
解:(1)∠APC+∠PAB+∠PCD=360°.理由如下:过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,
∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD.理由如下:
过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,
∴∠APC=∠PAB+∠PCD.
故答案为:∠APC+∠PAB+∠PCD=360°;∠APC=∠PAB+∠PCD;∠APC+∠PAB+∠PCD=360°.
点评:此题考查了平行线的性质.注意掌握两直线平行,内错角相等,同位角相等,同旁内角互补与辅助线的添加方法是解此题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
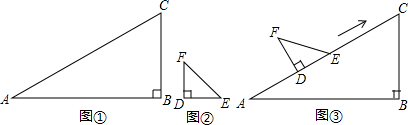
 如图,已知:正方形ABCD,由顶点A引两条射线分别交BC、CD于E、F,且∠EAF=45°,求证:BE+DF=EF.
如图,已知:正方形ABCD,由顶点A引两条射线分别交BC、CD于E、F,且∠EAF=45°,求证:BE+DF=EF.
 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若以CEF为顶点的△与以ABC为顶点的三角形相似且AC=3,BC=4时,则AD的长为
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若以CEF为顶点的△与以ABC为顶点的三角形相似且AC=3,BC=4时,则AD的长为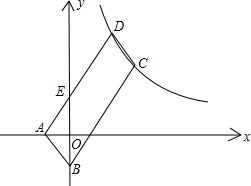 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=