题目内容
 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若以CEF为顶点的△与以ABC为顶点的三角形相似且AC=3,BC=4时,则AD的长为
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若以CEF为顶点的△与以ABC为顶点的三角形相似且AC=3,BC=4时,则AD的长为考点:翻折变换(折叠问题)
专题:
分析:若△CEF与△ABC相似,分两种情况:①若CE:CF=3:4,如图1所示,此时EF∥AB,CD为AB边上的高;②若CF:CE=3:4,如图2所示.由相似三角形角之间的关系,可以推出∠A=∠ECD与∠B=∠FCD,从而得到CD=AD=BD,即D点为AB的中点.
解答: 解:若△CEF与△ABC相似,分两种情况:
解:若△CEF与△ABC相似,分两种情况:
①若CE:CF=3:4,如图1所示.
∵CE:CF=AC:BC,
∴EF∥AB.
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高.
在Rt△ABC中,∵∠ACB=90°,AC=3,BC=4,
∴AB=
=5,
∴cosA=
=
,
 ∴AD=AC•cosA=3×
∴AD=AC•cosA=3×
=1.8;
②若CF:CE=3:4,如图2所示.
∵△CEF∽△CBA,
∴∠CEF=∠B.
由折叠性质可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠A=∠ECD,
∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴D点为AB的中点,
∴AD=
AB=
×5=2.5.
综上所述,AD的长为1.8或2.5.
故答案为1.8或2.5.
 解:若△CEF与△ABC相似,分两种情况:
解:若△CEF与△ABC相似,分两种情况:①若CE:CF=3:4,如图1所示.
∵CE:CF=AC:BC,
∴EF∥AB.
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高.
在Rt△ABC中,∵∠ACB=90°,AC=3,BC=4,
∴AB=
| AC2+BC2 |
∴cosA=
| AC |
| AB |
| 3 |
| 5 |
 ∴AD=AC•cosA=3×
∴AD=AC•cosA=3×| 3 |
| 5 |
②若CF:CE=3:4,如图2所示.
∵△CEF∽△CBA,
∴∠CEF=∠B.
由折叠性质可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠A=∠ECD,
∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴D点为AB的中点,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,AD的长为1.8或2.5.
故答案为1.8或2.5.
点评:本题主要考查了折叠的性质,勾股定理和相似三角形的判定与性质,难度适中.运用分类讨论及数形结合思想是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
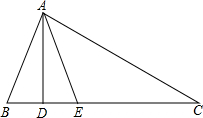 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.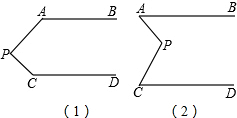 如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.
如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.
 如图,菱形ABCD的顶点A、顶点B均在x轴的正半轴上,AB=4,∠DAB=60°,将菱形ABCD沿AD翻折,得到菱形AEFD,若双曲线
如图,菱形ABCD的顶点A、顶点B均在x轴的正半轴上,AB=4,∠DAB=60°,将菱形ABCD沿AD翻折,得到菱形AEFD,若双曲线