题目内容
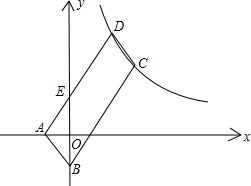 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=| k |
| x |
考点:平行四边形的性质,反比例函数图象上点的坐标特征
专题:
分析:分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=2,由此设C(m+1,n),D(m,n+2),C、D两点在双曲线y=
上,则(m+1)n=m(n+2),解得n=2m,设直线AD解析式为y=ax+b,将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=8S△ABE,列方程求m、n的值,根据k=(m+1)n求解.
| k |
| x |
解答: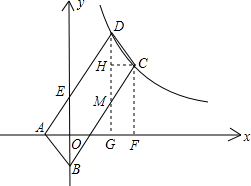 解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2,设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,
解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
,
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则
,
∴y=2x+2,E(0,2),BE=4,
∴S△ABE=
×BE×AO=2,
∵S四边形BCDE=8S△ABE=8×
×4×1=16,
∴S四边形BCDE=S△ABE+S四边形BEDM=16,
即2+4×m=16,
解得m=
,
∴n=2m=7,
∴k=(m+1)n=
×7=
.
故答案为:
.
 解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2,设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,
解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
|
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则
|
∴y=2x+2,E(0,2),BE=4,
∴S△ABE=
| 1 |
| 2 |
∵S四边形BCDE=8S△ABE=8×
| 1 |
| 2 |
∴S四边形BCDE=S△ABE+S四边形BEDM=16,
即2+4×m=16,
解得m=
| 7 |
| 2 |
∴n=2m=7,
∴k=(m+1)n=
| 9 |
| 2 |
| 63 |
| 2 |
故答案为:
| 63 |
| 2 |
点评:本题考查了反比例函数的综合运用.关键是通过作辅助线,将图形分割,寻找全等三角形,利用边的关系设双曲线上点的坐标,根据面积关系,列方程求解.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
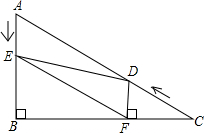 如图,在Rt△ABC中,∠B=90°,BC=
如图,在Rt△ABC中,∠B=90°,BC=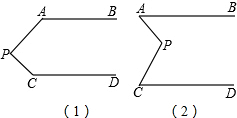 如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.
如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.