题目内容
现有一副三角板,如图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°;图③中,将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动(移动开始时点D与点A重合).
(1)△DEF在移动的过程中,若D、E两点始终在AC边上,
①F、C两点间的距离逐渐 ;连接FC,∠FCE的度数逐渐 .(填“不变”、“变大”或“变小”)
②∠FCE与∠CFE度数之和是否为定值,请加以说明;
(2)△DEF在移动的过程中,如果D、E两点在AC的延长线上,那么∠FCE与∠CFE之间又有怎样的数量关系,请直接写出结论;
(3)能否将△DEF移动至某位置,使F、C的连线与BC垂直?求出∠CFE的度数.
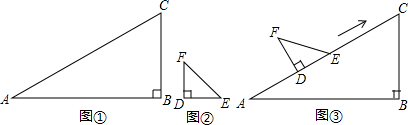
(1)△DEF在移动的过程中,若D、E两点始终在AC边上,
①F、C两点间的距离逐渐
②∠FCE与∠CFE度数之和是否为定值,请加以说明;
(2)△DEF在移动的过程中,如果D、E两点在AC的延长线上,那么∠FCE与∠CFE之间又有怎样的数量关系,请直接写出结论;
(3)能否将△DEF移动至某位置,使F、C的连线与BC垂直?求出∠CFE的度数.

考点:平移的性质,垂线,三角形的外角性质
专题:
分析:(1)①利用图形的变化得出F、C两点间的距离变化和,∠FCE的度数变化规律;
②利用外角的性质得出∠FCE+∠CFE=∠FED=45°,即可得出答案;
(2)利用外角的性质得出∠FCE+∠CFE=∠FEG=135°,即可得出答案;
(3)要使FC⊥BC,则需∠FCE=∠A=30°,进而得出∠CFE的度数.
②利用外角的性质得出∠FCE+∠CFE=∠FED=45°,即可得出答案;
(2)利用外角的性质得出∠FCE+∠CFE=∠FEG=135°,即可得出答案;
(3)要使FC⊥BC,则需∠FCE=∠A=30°,进而得出∠CFE的度数.
解答:解:(1)①F、C两点间的距离逐渐变小;连接FC,∠FCE的度数逐渐变大;
故答案为:变小,变大;
②∠FCE与∠CFE度数之和为定值;
理由:∵∠D=90°,∠DFE=45°,
又∵∠D+∠DFE+∠FED=180°,
∴∠FED=45°,
∵∠FED是△FEC的外角,
∴∠FCE+∠CFE=∠FED=45°,
即∠FCE与∠CFE度数之和为定值;
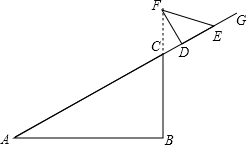
(2)如图,∠FCE与∠CFE度数之和为定值;
理由:∵∠FDE=90°,∠F=45°,
又∵∠FDE+∠F+∠FED=180°,
∴∠FED=45°,
∵∠FEG是△FEC的外角,
∴∠FCE+∠CFE=∠FEG=135°,
即∠FCE与∠CFE度数之和为定值;
(3)要使FC⊥BC,则需∠FCE=∠A=30°,
又∵∠CFE+∠FCE=45°,
∴∠CFE=45°-30°=15°.
故答案为:变小,变大;
②∠FCE与∠CFE度数之和为定值;
理由:∵∠D=90°,∠DFE=45°,
又∵∠D+∠DFE+∠FED=180°,
∴∠FED=45°,
∵∠FED是△FEC的外角,
∴∠FCE+∠CFE=∠FED=45°,
即∠FCE与∠CFE度数之和为定值;

(2)如图,∠FCE与∠CFE度数之和为定值;
理由:∵∠FDE=90°,∠F=45°,
又∵∠FDE+∠F+∠FED=180°,
∴∠FED=45°,
∵∠FEG是△FEC的外角,
∴∠FCE+∠CFE=∠FEG=135°,
即∠FCE与∠CFE度数之和为定值;
(3)要使FC⊥BC,则需∠FCE=∠A=30°,
又∵∠CFE+∠FCE=45°,
∴∠CFE=45°-30°=15°.
点评:此题主要考查了三角形的外角以及平行线的判定和三角形内角和定理等知识,熟练利用相关定理是解题关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 如图,在Rt△ABC中,∠B=90°,BC=
如图,在Rt△ABC中,∠B=90°,BC= 作图:请在所给的数轴上作出表示
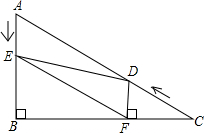
作图:请在所给的数轴上作出表示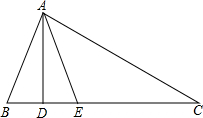 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.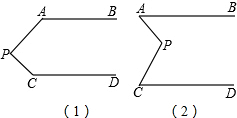 如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.
如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.