题目内容
 如图,已知:正方形ABCD,由顶点A引两条射线分别交BC、CD于E、F,且∠EAF=45°,求证:BE+DF=EF.
如图,已知:正方形ABCD,由顶点A引两条射线分别交BC、CD于E、F,且∠EAF=45°,求证:BE+DF=EF.考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:延长CD到G,使DG=BE,利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等可得AG=AE,全等三角形对应角相等可得∠DAG=∠BAE,然后求出∠EAF=∠GAF,再利用“边角边”证明△AEF和△AGF全等,根据全等三角形对应边相等可得EF=GF,然后结合图形整理即可得证.
解答: 证明:如图,延长CD到G,使DG=BE,
证明:如图,延长CD到G,使DG=BE,
在正方形ABCD中,AB=AD,∠B=∠ADC=90°,
∴∠ADG=∠B,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AG=AE,∠DAG=∠BAE,
∵∠EAF=45°,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-45°=45°,
∴∠EAF=∠GAF,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=GF,
∵GF=DG+DF=BE+DF,
∴BE+DF=EF.
 证明:如图,延长CD到G,使DG=BE,
证明:如图,延长CD到G,使DG=BE,在正方形ABCD中,AB=AD,∠B=∠ADC=90°,
∴∠ADG=∠B,
在△ABE和△ADG中,
|
∴△ABE≌△ADG(SAS),
∴AG=AE,∠DAG=∠BAE,
∵∠EAF=45°,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-45°=45°,
∴∠EAF=∠GAF,
在△AEF和△AGF中,
|
∴△AEF≌△AGF(SAS),
∴EF=GF,
∵GF=DG+DF=BE+DF,
∴BE+DF=EF.
点评:本题考查了全等三角形的判定与性质,正方形的性质,熟记三角形全等的判定方法和正方形的性质并作辅助线构造成全等三角形是解题的关键,也是本题的难点.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
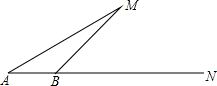 某轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,在小岛M周围120米以内有暗礁,若轮船不改变航向继续前进,有没有触礁的危险?请说明理由.
某轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,在小岛M周围120米以内有暗礁,若轮船不改变航向继续前进,有没有触礁的危险?请说明理由.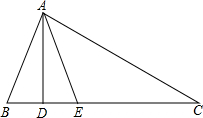 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=76°,∠C=26°.


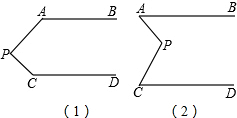 如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.
如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.
 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.理由是
如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.理由是