题目内容
当抛物线的解析式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1①有y=(x-m)2+2m-1②,所以抛物线顶点坐标为(m,2m-1),即x=m③,y=2m-1④.当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.将③代入④,得y=2x-1⑤.可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式:y=2x-1;
(1)根据上述阅读材料提供的方法,确定点(-2m,m-1)满足的函数关系式为 .
(2)根据阅读材料提供的方法,确定抛物线y=x2-
x+1+m+
顶点的纵坐标y与横坐标x之间的关系式.
(1)根据上述阅读材料提供的方法,确定点(-2m,m-1)满足的函数关系式为
(2)根据阅读材料提供的方法,确定抛物线y=x2-
| 2 |
| m |
| 1 |
| m2 |
考点:二次函数的性质
专题:
分析:(1)令x=-2m①,y=m-1②,由①得出m=-
x③,将③代入②,即可确定点(-2m,m-1)满足的函数关系式;
(2)根据材料提示,先把抛物线解析式配方成顶点式,写出顶点的表达式,再消掉字母m即可得到顶点的纵坐标y与横坐标x之间的关系式.
| 1 |
| 2 |
(2)根据材料提示,先把抛物线解析式配方成顶点式,写出顶点的表达式,再消掉字母m即可得到顶点的纵坐标y与横坐标x之间的关系式.
解答:解:(1)令x=-2m①,y=m-1②,
由①得m=-
x③,
将③代入②,得y=-
x-1,
即点(-2m,m-1)满足的函数关系式为y=-
x-1.
故答案为y=-
x-1;
(2)∵y=x2-
x+1+m+
=(x2-
x+
)+m+1
=(x-
)2+m+1,
∴抛物线的顶点坐标为(
,m+1),
设顶点为P(x,y),则x=
①,y=m+1②,
由①得出m=
③,
将③代入②,得y=
+1.
∴顶点的纵坐标y与横坐标x之间的关系式为y=
+1.
由①得m=-
| 1 |
| 2 |
将③代入②,得y=-
| 1 |
| 2 |
即点(-2m,m-1)满足的函数关系式为y=-
| 1 |
| 2 |
故答案为y=-
| 1 |
| 2 |
(2)∵y=x2-
| 2 |
| m |
| 1 |
| m2 |
=(x2-
| 2 |
| m |
| 1 |
| m2 |
=(x-
| 1 |
| m |
∴抛物线的顶点坐标为(
| 1 |
| m |
设顶点为P(x,y),则x=
| 1 |
| m |
由①得出m=
| 1 |
| x |
将③代入②,得y=
| 1 |
| x |
∴顶点的纵坐标y与横坐标x之间的关系式为y=
| 1 |
| x |
点评:本题考查了二次函数的性质,函数解析式一般形式与顶点式的转化,读懂材料提供的信息,写出顶点的坐标,并会消掉字母m是解题的关键,灵活性较强,有创意.

练习册系列答案
相关题目
 如图是某公司四个部门的营业情况,则销售情况最好的是( )
如图是某公司四个部门的营业情况,则销售情况最好的是( )| A、甲 | B、乙 | C、丙 | D、丁 |
 如图,点A(3,0),B(0,
如图,点A(3,0),B(0,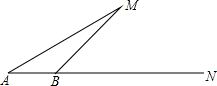 某轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,在小岛M周围120米以内有暗礁,若轮船不改变航向继续前进,有没有触礁的危险?请说明理由.
某轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,在小岛M周围120米以内有暗礁,若轮船不改变航向继续前进,有没有触礁的危险?请说明理由.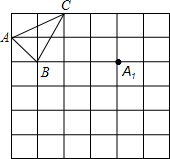 作图题:如图是6×6的网格,已知格点△ABC和格点A1.
作图题:如图是6×6的网格,已知格点△ABC和格点A1.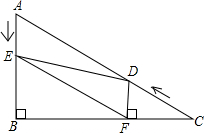 如图,在Rt△ABC中,∠B=90°,BC=
如图,在Rt△ABC中,∠B=90°,BC=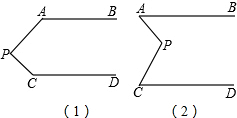 如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.
如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB,∠PCD的关系,请你从所得两个结论中任意选出一个,说明你所探究的结论的正确性.