题目内容
15.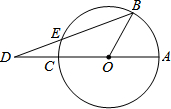 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )| A. | DE=EB | B. | $\sqrt{2}$DE=EB | C. | $\sqrt{3}$DE=DO | D. | DE=OB |
分析 连接EO,只要证明∠D=∠EOD即可解决问题.
解答 解: 连接EO.
连接EO.
∵OB=OE,
∴∠B=∠OEB,
∵∠OEB=∠D+∠DOE,∠AOB=3∠D,
∴∠B+∠D=3∠D,
∴∠D+∠DOE+∠D=3∠D,
∴∠DOE=∠D,
∴ED=EO=OB,
故选D.
A、错误.假设DE=EB,则△EOB是等边三角形,则∠AOB=3∠D=90°,OB⊥AD,显然与题目不符.
B、错误.假设$\sqrt{2}$DE=EB,则△EOB是等腰直角三角形,则∠AOB=3∠D=67.5°,显然与题目不符.
C、错误.假设$\sqrt{3}$DE=EB,则△EOB是等腰三角形,且底角∠B=30°,则∠AOB=45°,显然不符合题意.
点评 本题考查圆的有关知识、三角形的外角等知识,解题的关键是添加除以辅助线,利用等腰三角形的判定方法解决问题,属于中考常考题型.

练习册系列答案
相关题目
3.定义:若点P(a,b)在函数y=$\frac{1}{x}$的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=$\frac{1}{x}$的一个“派生函数”.例如:点(2,$\frac{1}{2}$)在函数y=$\frac{1}{x}$的图象上,则函数y=2x2+$\frac{1}{2}x$称为函数y=$\frac{1}{x}$的一个“派生函数”.现给出以下两个命题:
(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
| A. | 命题(1)与命题(2)都是真命题 | B. | 命题(1)与命题(2)都是假命题 | ||
| C. | 命题(1)是假命题,命题(2)是真命题 | D. | 命题(1)是真命题,命题(2)是假命题 |
10.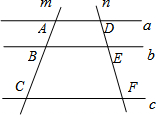 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )
如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )
 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )
如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
20.六边形的内角和是( )
| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
7.若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,则x的值为( )
| A. | 1 | B. | 6 | C. | 1或6 | D. | 5或6 |
4. 如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
 如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )| A. | 15° | B. | 30° | C. | 60° | D. | 75° |