题目内容
11.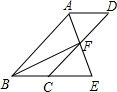 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
分析 (1)由平行四边形的性质和角平分线得出∠BAE=∠BEA,即可得出AB=BE;
(2)先证明△ABE是等边三角形,得出AE=AB=4,AF=EF=2,由勾股定理求出BF,由AAS证明△ADF≌△ECF,得出△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=$\frac{1}{2}$AE•BF,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF=$\sqrt{A{B}^{2}-A{F}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
$\left\{\begin{array}{l}{∠D=∠ECF}&{\;}\\{∠DAF=∠E}&{\;}\\{AF=EF}&{\;}\end{array}\right.$,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=$\frac{1}{2}$AE•BF=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$.
点评 此题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定、等边三角形的判定与性质、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题(2)的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
1. 如图,⊙O的圆心角∠BOC=112°,点D在弦BA的延长线上且AD=AC,则∠D的度数为( )
如图,⊙O的圆心角∠BOC=112°,点D在弦BA的延长线上且AD=AC,则∠D的度数为( )
 如图,⊙O的圆心角∠BOC=112°,点D在弦BA的延长线上且AD=AC,则∠D的度数为( )
如图,⊙O的圆心角∠BOC=112°,点D在弦BA的延长线上且AD=AC,则∠D的度数为( )| A. | 28° | B. | 56° | C. | 30° | D. | 41° |
3.定义:若点P(a,b)在函数y=$\frac{1}{x}$的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=$\frac{1}{x}$的一个“派生函数”.例如:点(2,$\frac{1}{2}$)在函数y=$\frac{1}{x}$的图象上,则函数y=2x2+$\frac{1}{2}x$称为函数y=$\frac{1}{x}$的一个“派生函数”.现给出以下两个命题:
(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
| A. | 命题(1)与命题(2)都是真命题 | B. | 命题(1)与命题(2)都是假命题 | ||
| C. | 命题(1)是假命题,命题(2)是真命题 | D. | 命题(1)是真命题,命题(2)是假命题 |
20.六边形的内角和是( )
| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
 在一个不透明的布袋中装有三个小球,小球上分别标有数字-1、0、2,它们除了数字不同外,其他都完全相同.
在一个不透明的布袋中装有三个小球,小球上分别标有数字-1、0、2,它们除了数字不同外,其他都完全相同.


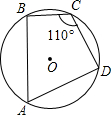 如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70度.
如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70度.