题目内容
18. 如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
分析 求出AD=BC,根据ASA推出△AED≌△BFC,根据全等三角形的性质得出即可.
解答 证明:∵AC=BD,
∴AC+CD=BD+CD,
∴AD=BC,
在△AED和△BFC中,
$\left\{\begin{array}{l}{∠A=∠B}\\{AD=BC}\\{∠ADE=∠BCF}\end{array}\right.$,
∴△AED≌△BFC(ASA),
∴DE=CF.
点评 本题考查了全等三角形的性质和判定的应用,能求出△AED≌△BFC是解此题的关键,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
13. 如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )
如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )
 如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )
如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
3.定义:若点P(a,b)在函数y=$\frac{1}{x}$的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=$\frac{1}{x}$的一个“派生函数”.例如:点(2,$\frac{1}{2}$)在函数y=$\frac{1}{x}$的图象上,则函数y=2x2+$\frac{1}{2}x$称为函数y=$\frac{1}{x}$的一个“派生函数”.现给出以下两个命题:
(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
| A. | 命题(1)与命题(2)都是真命题 | B. | 命题(1)与命题(2)都是假命题 | ||
| C. | 命题(1)是假命题,命题(2)是真命题 | D. | 命题(1)是真命题,命题(2)是假命题 |
10.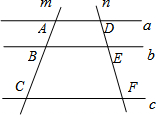 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )
如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )
 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )
如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
7.若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,则x的值为( )
| A. | 1 | B. | 6 | C. | 1或6 | D. | 5或6 |
3.x4-9因式分解正确的是( )
| A. | (x2+3)(x2-3) | B. | (x2+3)(x+3)(x-3) | C. | (x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$) | D. | (x2+3)(x-$\sqrt{3}$) |