题目内容
8.已知xm=9,xn=3,则xm-3n的值为=$\frac{1}{3}$.分析 根据同底数幂的除法法则及幂的乘方法则把原式化为xm÷(xn)3,再把xm=9,xn=3代入求值即可.
解答 解:∵xm=9,xn=3,
∴xm-3n=xm÷(xn)3=9÷33=9÷27=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查的是同底数幂的除法,熟知同底数幂的除法法则及幂的乘方法则是解答此题的关键.

练习册系列答案
相关题目
3.定义:若点P(a,b)在函数y=$\frac{1}{x}$的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=$\frac{1}{x}$的一个“派生函数”.例如:点(2,$\frac{1}{2}$)在函数y=$\frac{1}{x}$的图象上,则函数y=2x2+$\frac{1}{2}x$称为函数y=$\frac{1}{x}$的一个“派生函数”.现给出以下两个命题:
(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
| A. | 命题(1)与命题(2)都是真命题 | B. | 命题(1)与命题(2)都是假命题 | ||
| C. | 命题(1)是假命题,命题(2)是真命题 | D. | 命题(1)是真命题,命题(2)是假命题 |
4. 如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
 如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )| A. | 15° | B. | 30° | C. | 60° | D. | 75° |
3.x4-9因式分解正确的是( )
| A. | (x2+3)(x2-3) | B. | (x2+3)(x+3)(x-3) | C. | (x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$) | D. | (x2+3)(x-$\sqrt{3}$) |
13.下列计算正确的是( )
| A. | 3x2-2x2=1 | B. | x+x=x2 | C. | 4x8÷2x2=2x4 | D. | x•x=x2 |
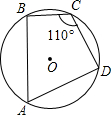 如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70度.
如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70度.
 在矩形纸片ABCD中,AE=CG=$\sqrt{3}$,点P,Q分别是在边AB,CD上,BP=DQ,将△BGP和△DEQ分别沿PG,EQ翻折,点D,B的对应点分别是D′,B′,若四边形ED′GB′是有一边平行于AB的菱形(如图甲或图乙所示),且∠D′EB′=30°,则AP的长是2$\sqrt{3}$+1或3.
在矩形纸片ABCD中,AE=CG=$\sqrt{3}$,点P,Q分别是在边AB,CD上,BP=DQ,将△BGP和△DEQ分别沿PG,EQ翻折,点D,B的对应点分别是D′,B′,若四边形ED′GB′是有一边平行于AB的菱形(如图甲或图乙所示),且∠D′EB′=30°,则AP的长是2$\sqrt{3}$+1或3.