题目内容
7. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则cos∠ABC的值是$\frac{\sqrt{195}}{25}$.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则cos∠ABC的值是$\frac{\sqrt{195}}{25}$.
分析 利用“割补法”求出△ABC的面积,作AG⊥BC,利用面积不变,求出AG的长,再求出cos∠ABC的值.
解答 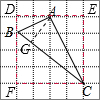 解:补出如图正方形DECF,作AG⊥BC.
解:补出如图正方形DECF,作AG⊥BC.
则S△ABC=S正方形DECF-S△ABD-S△AEC-S△BCF,
=16-1-4-8=3,
又∵BC=$\sqrt{{4}^{2}+{3}^{2}}$=5,AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$;
∴$\frac{1}{2}$×5AG=3,
∴AG=$\frac{6}{5}$,
∴sin∠ABC=$\frac{6}{5\sqrt{5}}$,
∴cos∠ABC=$\sqrt{1-(\frac{6}{5\sqrt{5}})^{2}}$=$\frac{\sqrt{195}}{25}$,
故答案为$\frac{\sqrt{195}}{25}$.
点评 本题考查了锐角三角函数的定义,从图中找到所需的值是解题的关键.

练习册系列答案
相关题目
17. 如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )
如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )
 如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )
如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )| A. | $\frac{125}{12}$ | B. | $\frac{125}{24}$ | C. | 40 | D. | 20 |
 如图,正方形ABCD中,点M沿A-D-C运动到C,AN⊥BM,点P为AN的中点,AB=4,则点P的运动的路径长为4.
如图,正方形ABCD中,点M沿A-D-C运动到C,AN⊥BM,点P为AN的中点,AB=4,则点P的运动的路径长为4.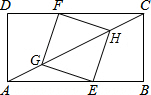 如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.
如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$. 如图.将三角形ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,则∠BCB′的度数是20°.
如图.将三角形ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,则∠BCB′的度数是20°. 如图,已知:G是△ABC的重心,GE∥AC,则DE:BD=1:3.
如图,已知:G是△ABC的重心,GE∥AC,则DE:BD=1:3.