题目内容
6.某商场设立一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 $\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
(2)画出获得铅笔频率的折线统计图;
(3)请估计,当n很大时,落在“铅笔”区域的频率将会在哪一个数的附近摆动?
(4)假如你去转动该转盘一次,你获得铅笔的概率有多大?
分析 (1)根据频率公式可以计算空格要填的数据;
(2)根据(1)中所求,得出获得“三等奖”频率的折线统计图即可;
(3)根据计算出的频率求出平均值即为转盘的次数n很大概率的接近值..
解答 解:(1)
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
(2)如图所示:
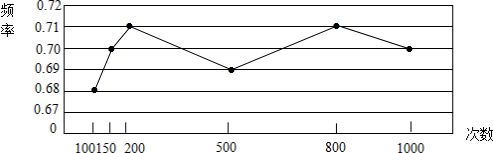
(3)当转动转盘的次数n很大时,概率将会接近(0.68+0.70+0.71+0.69+0.71+0.70)÷6≈0.70.
故答案为:0.70;
(4)∵当n很大时,落在“铅笔”区域的频率在0.70附近摆动,
∴获得铅笔的概率是0.70.
点评 本题考查的是利用频率估计概率,正确理解频率与概率之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列函数中,y随x增大而减小的是( )
| A. | y=$\frac{2}{x}$ | B. | y=$\frac{-2}{x}$ | C. | y=-2x+4 | D. | y=4+2x |
 如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.
如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ. 如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.
如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.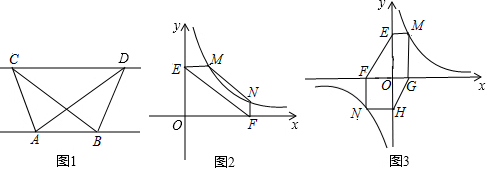
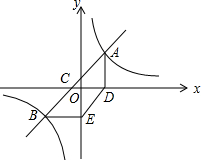 如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E.
如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E.