题目内容
1. 如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.
如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.(1)当t=2s时,求直线l的函数表达式;
(2)如果点M(a,3),当OM是Rt△OPB斜边PB上的中线时,在备用图中画出图形,并分别求出t和a的值;
(3)直接写出t为何值时,直线l与双曲线y=$\frac{4}{x}$(x>0)有且仅有一个公共点.
分析 (1)先求出AP进而得出OP即可求出b;
(2)先确定出直线l的解析式,进而求出点B,P的坐标,利用中点坐标即可得出t,a的值;
(3)联立直线l和双曲线建立方程用△=0,即可求出t的值.
解答 解:(1)当t=2时,AP=2×1=2
∵A(0,2),
∴OA=2,
∴OP=OA+AP=2+2=4,
∴直线l的解析式为y=-2x+4;
(2)如图,
由运动知,AP=t,
∴OP=OA+AP=t+2,
∴直线l的解析式为y=-2x+t+2,
∴P(0,t+2),B($\frac{t+2}{2}$,0),
∵OM是Rt△OPB的斜边PB上的中线,
∴M(a,3)是PB的中点,
∴$\frac{t+2}{2}$=2a,t+2=3×2,
∴t=4,a=$\frac{3}{2}$
(3)由(2)知,直线l的解析式为y=-2x+t+2①,
∵双曲线y=$\frac{4}{x}$②,
联立①②化简得,2x2-(t+2)x+4=0,
∵直线l与双曲线y=$\frac{4}{x}$(x>0)有且仅有一个公共点.
∴△=(t+2)2-4×2×4=0,
∴t=-2+4$\sqrt{2}$或t=-2-4$\sqrt{2}$(舍),
即:t=-2+4$\sqrt{2}$时,直线l与双曲线y=$\frac{4}{x}$(x>0)有且仅有一个公共点.
点评 此题是反比例函数综合题,主要考查了待定系数法,直角三角形的性质,一元二次方程根的情况,解(1)的关键是求出OP,解(2)的关键是求出点B,P的坐标,解(3)的关键是用一元二次方程根的判别式建立方程求解.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
11.我们约定“&”一个实际意义,规定m&n=$\sqrt{m}$×$\sqrt{n}$-$\sqrt{\frac{m}{n}}$,则2&3的值为( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{6}}}{3}$ | C. | $\sqrt{6}$ | D. | $\frac{{4\sqrt{6}}}{3}$ |
12.已知函数y=x+b的图象与坐标轴围成的三角形面积为1,则b=( )
| A. | ±$\sqrt{2}$ | B. | ±2 | C. | 2 | D. | $\sqrt{2}$ |
6.某商场设立一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:
(1)计算并完成表格;
(2)画出获得铅笔频率的折线统计图;
(3)请估计,当n很大时,落在“铅笔”区域的频率将会在哪一个数的附近摆动?
(4)假如你去转动该转盘一次,你获得铅笔的概率有多大?
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 $\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
(2)画出获得铅笔频率的折线统计图;
(3)请估计,当n很大时,落在“铅笔”区域的频率将会在哪一个数的附近摆动?
(4)假如你去转动该转盘一次,你获得铅笔的概率有多大?
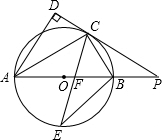 如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE. 某笔直河道上有甲、乙两港,相距120千米,一艘轮船从甲港出发,顺流航行4小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发3小时后从乙港出发,逆流航行3小时到达甲港,并立即返回(掉头时间忽略不计).已知水流速度是5千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船行驶时间x(小时)之间的函数关系,结合图象解答下列问题:(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)
某笔直河道上有甲、乙两港,相距120千米,一艘轮船从甲港出发,顺流航行4小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发3小时后从乙港出发,逆流航行3小时到达甲港,并立即返回(掉头时间忽略不计).已知水流速度是5千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船行驶时间x(小时)之间的函数关系,结合图象解答下列问题:(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度) 如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数$\frac{k}{x}$(k≠0)的图象交于A、B两点.与y轴交于点C,过点B作BD⊥y轴于点D.己CD=3,tan∠BCD=$\frac{2}{3}$.点B的坐标为(m,-1).
如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数$\frac{k}{x}$(k≠0)的图象交于A、B两点.与y轴交于点C,过点B作BD⊥y轴于点D.己CD=3,tan∠BCD=$\frac{2}{3}$.点B的坐标为(m,-1).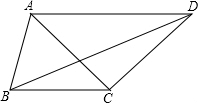 如图,在△ACD中,∠ACD=90°,AC=DC,∠ABC=75°,若AB=3$\sqrt{2}$,BC=5,则BD的长为7$\sqrt{2}$.
如图,在△ACD中,∠ACD=90°,AC=DC,∠ABC=75°,若AB=3$\sqrt{2}$,BC=5,则BD的长为7$\sqrt{2}$.