题目内容
17.阅读下面的文字,解答问题大家知道$\sqrt{2}$是无理数,而无理数是无限不循环小数,因此$\sqrt{2}$的小数部分我们不可能全部地写出来,但是由于
1<$\sqrt{2}$<2,所以$\sqrt{2}$的整数部分为1,将$\sqrt{2}$减去其整数部分1,所得的差就是其小数部分$\sqrt{2}$-1,根据以上的内容,解答下面的问题:
(1)$\sqrt{5}$的整数部分是2,小数部分是$\sqrt{5}$-2;
(2)1+$\sqrt{2}$的整数部分是2,小数部分是$\sqrt{2}$-1;
(3)1+$\sqrt{2}$+$\sqrt{3}$整数部分是4,小数部分是$\sqrt{2}$+$\sqrt{3}$-3;
(4)若设2+$\sqrt{3}$整数部分是x,小数部分是y,求x-$\sqrt{3}$y的值.
分析 (1)先估算出$\sqrt{5}$的范围,即可得出答案;
(2)先估算出$\sqrt{2}$的范围,即可得出答案;
(3)先求出1+$\sqrt{2}$+$\sqrt{3}$的范围,即可得出答案;
(4)先求出2+$\sqrt{3}$的范围,求出x、y,即可得出答案.
解答 解:(1)∵2<$\sqrt{5}$<3,
∴$\sqrt{5}$的整数部分是2,小数部分为$\sqrt{5}$-2,
故答案为:2,$\sqrt{5}$-2;
(2)∵1<$\sqrt{2}$<2,
∴2<1+$\sqrt{2}$<3,
∴1+$\sqrt{2}$的整数部分是2,小数部分是1+$\sqrt{2}$-2=$\sqrt{2}$-1,
故答案为:2,$\sqrt{2}$-1;
(3)∵2.4<1+$\sqrt{2}$<3,1.7$<\sqrt{3}<2$,
∴4.1<1+$\sqrt{2}$+$\sqrt{3}$<5,
∴1+$\sqrt{2}$+$\sqrt{3}$,的整数部分是4,小数部分是$\sqrt{2}$+$\sqrt{3}$-3,
故答案为:4,$\sqrt{2}$+$\sqrt{3}$-3;
(4)∵1<$\sqrt{3}$<2,
∴3<2+$\sqrt{3}$<4,
∴x=3,y=$\sqrt{3}$-1,
∴x-$\sqrt{3}$y=3-$\sqrt{3}$($\sqrt{3}$-1)=$\sqrt{3}$.
点评 本题考查了估算无理数的大小,能正确估算出每个无理数的大小是解此题的关键.

练习册系列答案
相关题目
5.若式子3a-4的值不小于2,则a的取值范围是( )
| A. | a≥-$\frac{2}{3}$ | B. | a≥2 | C. | a<-$\frac{2}{3}$ | D. | a≤2 |
12.已知函数y=x+b的图象与坐标轴围成的三角形面积为1,则b=( )
| A. | ±$\sqrt{2}$ | B. | ±2 | C. | 2 | D. | $\sqrt{2}$ |
6.某商场设立一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:
(1)计算并完成表格;
(2)画出获得铅笔频率的折线统计图;
(3)请估计,当n很大时,落在“铅笔”区域的频率将会在哪一个数的附近摆动?
(4)假如你去转动该转盘一次,你获得铅笔的概率有多大?
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 $\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
(2)画出获得铅笔频率的折线统计图;
(3)请估计,当n很大时,落在“铅笔”区域的频率将会在哪一个数的附近摆动?
(4)假如你去转动该转盘一次,你获得铅笔的概率有多大?
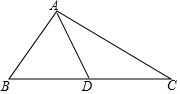 如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=$\frac{11}{10}$,则tan∠BAD=$\frac{33}{10}$.
如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=$\frac{11}{10}$,则tan∠BAD=$\frac{33}{10}$.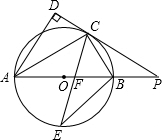 如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.