题目内容
11.(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.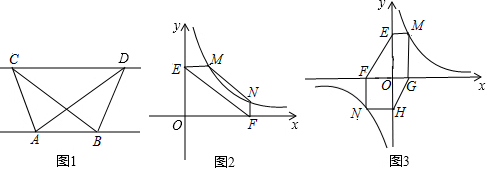
(2)结论应用:
①如图2,点M、N在反比例函数y=$\frac{k}{x}$(k>0)的图象上,过点M作ME⊥y轴,垂足分别为E,F,试证明:MN∥EF;
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与EF是否平行.
分析 (1)先判断出CG∥DH,再利用三角形ABC和三角形ABD的面积相等,得出CG=DH即可得出结论;
(2)①先求出三角形EFM的面积,再求出三角形EFN的面积,即可得出三角形EFM和三角形EFN的面积相等,最后利用(1)的结论得出MN∥EF;
②利用(1)的结论即可得出结论.
解答 解:(1)如图1,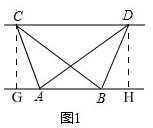 过点C作⊥AB于G,过点D作DH⊥AB于H,
过点C作⊥AB于G,过点D作DH⊥AB于H,
∴∠CGA=∠DHB=90°,
∴CG∥DH,
∵△ABC和△ABD的面积相等,
∴CG=DH,
∴四边形CGHD是平行四边形;
(2)①如图2,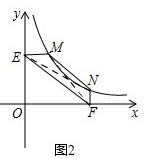 连接MF,NE,
连接MF,NE,
设M(x1,y1),N(x2,y2),
∵点M,N在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴x1y1=k,x2y2=k,
∵ME⊥y轴,NF⊥x轴,
∴OE=y1,OF=x2,
∴S△EFM=$\frac{1}{2}$x1•x2=$\frac{1}{2}$k,S△EFN=$\frac{1}{2}$x2y2=$\frac{1}{2}$k,
∴S△EFM=S△EFN,
由(1)中的结论可知,MN∥EF;
②MN∥EF,理由:如图3,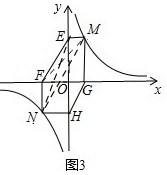 由(1)中的结论可知,MN∥EF.
由(1)中的结论可知,MN∥EF.
点评 此题是反比例函数综合题,主要考查了平行四边形的判定和性质,三角形的面积公式,解本题的关键是作出辅助线,判断出S△EFM=S△EFN,是一道中等难度的中考常考题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.某商场设立一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:
(1)计算并完成表格;
(2)画出获得铅笔频率的折线统计图;
(3)请估计,当n很大时,落在“铅笔”区域的频率将会在哪一个数的附近摆动?
(4)假如你去转动该转盘一次,你获得铅笔的概率有多大?
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 $\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
(2)画出获得铅笔频率的折线统计图;
(3)请估计,当n很大时,落在“铅笔”区域的频率将会在哪一个数的附近摆动?
(4)假如你去转动该转盘一次,你获得铅笔的概率有多大?
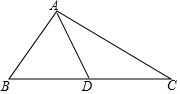 如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=$\frac{11}{10}$,则tan∠BAD=$\frac{33}{10}$.
如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=$\frac{11}{10}$,则tan∠BAD=$\frac{33}{10}$.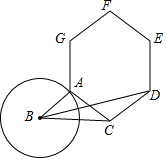 如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为$2\sqrt{3}+1$.
如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为$2\sqrt{3}+1$.