题目内容
9.先化简,再求值:$\frac{{x}^{2}}{x-3}$+$\frac{9}{3-x}$,其中x=$\sqrt{3}$-3.分析 先通分,再把分子相加,最后选取合适的x的值代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}}{x-3}$-$\frac{9}{x-3}$
=$\frac{{x}^{2}-9}{x-3}$
=x+3.
当x=$\sqrt{3}$-3时,原式=$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式的加减法则是解答此题的关键.

练习册系列答案
相关题目
19.下列各数是无理数的是( )
| A. | $\sqrt{4}$ | B. | -$\frac{1}{3}$ | C. | π | D. | -$\root{3}{8}$ |
17.下列运算中,正确的是( )
| A. | a2+a=2a3 | B. | a2•a3=a5 | C. | (a2)3=a5 | D. | (ab2)3=a3b2 |
4.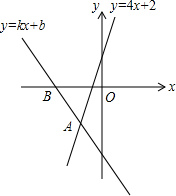 如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
 如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )| A. | -2<x<-1 | B. | -2$<x<-\frac{1}{2}$ | C. | -1$<x<-\frac{1}{2}$ | D. | -$\frac{1}{2}<x<0$ |
18.若am=2,an=3,则am+n的值为( )
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′. 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则AC的长为2.
如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则AC的长为2.