题目内容
16．
如图，在△ABC中，点E、F分别是AB、AC的中点，则下列结论不正确的是（ ）| A． | EF∥BC | B． | BC=2EF | C． | ∠AEF=∠B | D． | AE=AF |
分析 根据三角形中位线定理即可判断．
解答 解：∵AE=EB，AF=FC，
∴EF∥BC，EF=$\frac{1}{2}$BC，即BC=2EF，
∴∠AEF=∠B，
故A、B、C正确，D错误．
故选D．
点评 本题考查三角形中位线定理：三角形的中位线平行于第三边并且等于第三边的一半，解题的关键是记住三角形中位线定理，属于中考常考题型．
练习册系列答案
相关题目
7．
如图，已知直线a，b被直线c所截，则∠1和∠2是一对（ ）
如图，已知直线a，b被直线c所截，则∠1和∠2是一对（ ）| A． | 对顶角 | B． | 同位角 | C． | 内错角 | D． | 同旁内角 |
4．
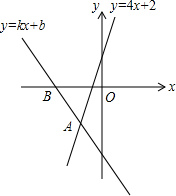如图，经过点B（-2，0）的直线y=kx+b与直线y=kx+b相交于点A（-1，-2），则不等式4x+2＜kx+b＜0的解集为（ ）
如图，经过点B（-2，0）的直线y=kx+b与直线y=kx+b相交于点A（-1，-2），则不等式4x+2＜kx+b＜0的解集为（ ）| A． | -2＜x＜-1 | B． | -2$＜x＜-\frac{1}{2}$ | C． | -1$＜x＜-\frac{1}{2}$ | D． | -$\frac{1}{2}＜x＜0$ |
11．城东中学七年级举行跳绳比赛，要求与每班选出5名学生参加，在规定时间每人跳绳不低于150次为优秀，冠、亚军在甲、乙两班中产生，如表是这两个班的5名学生的比赛数据（单位：次）
根据以上信息，解答下列问题：
（1）写出表中a的值和甲、乙两班的优秀率；
（2）写出两班比赛数据的中位数；
（3）你认为冠军奖应发给那个班？简要说明理由．
| 1号 | 2号 | 3号 | 4号 | 5号 | 平均次数 | 方差 | |
| 甲班 | 150 | 148 | 160 | 139 | 153 | 150 | 46.8 |
| 乙班 | 139 | 150 | 145 | 169 | 147 | a | 103.2 |
（1）写出表中a的值和甲、乙两班的优秀率；
（2）写出两班比赛数据的中位数；
（3）你认为冠军奖应发给那个班？简要说明理由．
如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′．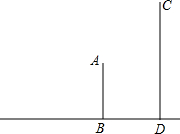
已知如图，从20米高的甲楼A望乙楼顶C处的仰角是30°，望乙楼底D处的俯角是45°，求乙楼的高度（精确到0.1米，$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．