题目内容
12. 如图,在四边形ABCD中,对角线AC、BD相交于O点,且AB=AD,CB=CD,则图中全等三角形共有(
如图,在四边形ABCD中,对角线AC、BD相交于O点,且AB=AD,CB=CD,则图中全等三角形共有(| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
分析 首先利用SSS判定△ABC≌△ADC,进而可得∠BAO=∠DAO,∠BCO=∠DCO,再利用SAS分别判定△ABO≌△ADO,△BCO≌△DCO.
解答 解:∵在△ABC和△ADC中$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠BAO=∠DAO,∠BCO=∠DCO,
∵在△ABO和△ADO中$\left\{\begin{array}{l}{AB=DA}\\{∠BAO=∠DAO}\\{AO=AO}\end{array}\right.$,
∴△ABO≌△ADO(SAS),
∵在△BCO和△DOC中$\left\{\begin{array}{l}{BC=DC}\\{∠BCO=∠DCO}\\{OC=OC}\end{array}\right.$,
∴△BCO≌△DCO(SAS),
共3对全等三角形,
故选:C.
点评 此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
2.下列四个图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.一次函数y=-2x-3的图象与y轴的交点坐标是( )
| A. | (3,0) | B. | (0,3) | C. | (-3,0) | D. | (0,-3) |
7. 如图,已知直线a,b被直线c所截,则∠1和∠2是一对( )
如图,已知直线a,b被直线c所截,则∠1和∠2是一对( )
 如图,已知直线a,b被直线c所截,则∠1和∠2是一对( )
如图,已知直线a,b被直线c所截,则∠1和∠2是一对( )| A. | 对顶角 | B. | 同位角 | C. | 内错角 | D. | 同旁内角 |
17.下列运算中,正确的是( )
| A. | a2+a=2a3 | B. | a2•a3=a5 | C. | (a2)3=a5 | D. | (ab2)3=a3b2 |
4.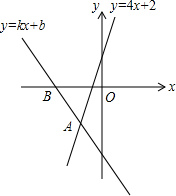 如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
 如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )| A. | -2<x<-1 | B. | -2$<x<-\frac{1}{2}$ | C. | -1$<x<-\frac{1}{2}$ | D. | -$\frac{1}{2}<x<0$ |
 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.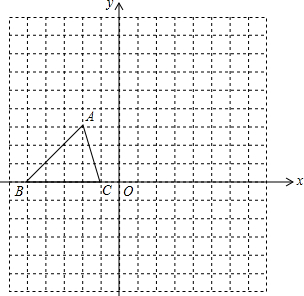 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).