题目内容
13．给出正三角形、正方形、正五边形、正六边形四种形状的地砖，若只能选购其中的一种地砖来铺满地面，则可供选择的地砖共有（ ）| A． | 4种 | B． | 3种 | C． | 2种 | D． | 1种 |
分析 由镶嵌的条件知，判断一种图形是否能够镶嵌，只要看一看正多边形的内角度数是否能整除360°，能整除的可以平面镶嵌，反之则不能．
解答 解：正三角形的每个内角是60°，能整除360°，6个能组成镶嵌；
正方形的每个内角是90°，4个能组成镶嵌；
正五边形每个内角是180°-360°÷5=108°，不能整除360°，不能镶嵌；
正六边形的每个内角是120°，能整除360°，3个能组成镶嵌；
故若只能选购其中的一种地砖来铺满地面，则可供选择的地砖共有3种．
故选B．
点评 此题主要考查了平面镶嵌，用一种正多边形的镶嵌应符合一个内角度数能整除360°．任意多边形能进行镶嵌，说明它的内角和应能整除360°．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
3．一次函数y=-2x-3的图象与y轴的交点坐标是（ ）
| A． | （3，0） | B． | （0，3） | C． | （-3，0） | D． | （0，-3） |
4．
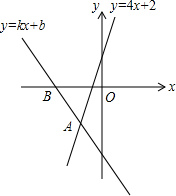如图，经过点B（-2，0）的直线y=kx+b与直线y=kx+b相交于点A（-1，-2），则不等式4x+2＜kx+b＜0的解集为（ ）
如图，经过点B（-2，0）的直线y=kx+b与直线y=kx+b相交于点A（-1，-2），则不等式4x+2＜kx+b＜0的解集为（ ）| A． | -2＜x＜-1 | B． | -2$＜x＜-\frac{1}{2}$ | C． | -1$＜x＜-\frac{1}{2}$ | D． | -$\frac{1}{2}＜x＜0$ |
如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′．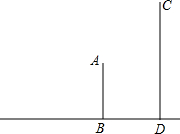
已知如图，从20米高的甲楼A望乙楼顶C处的仰角是30°，望乙楼底D处的俯角是45°，求乙楼的高度（精确到0.1米，$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．
18．若am=2，an=3，则am+n的值为（ ）
| A． | 5 | B． | 6 | C． | 8 | D． | 9 |
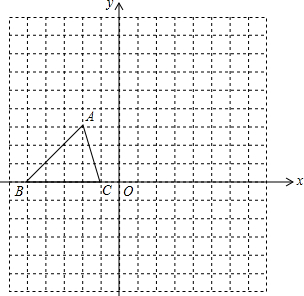如图所示，已知△ABC的三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0）．
已知：如图所示，E为正方形ABCD外一点，AE=AD，∠ADE=75°，求∠AEB的度数．