题目内容
14.例:如图①,平面直角坐标系xOy中有点B(2,3)和C(5,4),求△OBC的面积.解:过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.依题意,可得S△OBC=S梯形BDEC+S△OBD-S△OCE =$\frac{1}{2}$(BD+CE)(OE-OD)+$\frac{1}{2}$OD•BD-$\frac{1}{2}$OE•CE=$\frac{1}{2}$×(3+4)×(5-2)+$\frac{1}{2}$×2×3-$\frac{1}{2}$×5×4=3.5.
∴△OBC的面积为3.5.
(1)如图②,若B(3,y)、C(x,5)均为第一象限的点,O、B、C三点不在同一条直线上.仿照例题的解法,求△OBC的面积(用含x、y、的代数式表示);
(2)如图③,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.
(3)若三个点的坐标分别A(2,2)、B(4,0)、C(-2,a),△ABC的面积为12.求a的值,

分析 (1)△OBC的面积等于梯形BDEC的面积+△OBD的面积-△OCE的面积即可;
(2)根据(1)的特点先求出△OAB的面积,再求出△OBC的面积,最后求和即可;
(3)分点C在第二象限和第三现象两种情况,同(2)的方法计算即可.
解答 解:(1)如图②,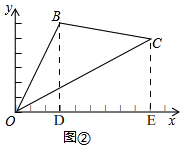
过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.依题意,可得
∵B(3,y)、C(x,5)
∴S△OBC=S梯形BDEC+S△OBD-S△OCE
=$\frac{1}{2}$(BD+CE)(OE-OD)+$\frac{1}{2}$OD•BD-$\frac{1}{2}$OE•CE
=$\frac{1}{2}$×(y+5)×(x-3)+$\frac{1}{2}$×3×y-$\frac{1}{2}$×x×5
=$\frac{1}{2}$xy-$\frac{15}{2}$.
(2)如图③,连接OB,过点A作AD⊥x轴于D,点B作BE⊥x轴于E,点C作CF⊥x轴于FM
∵三个点的坐标分别为A(2,5),B(7,7),C(9,1),
∴S四边形OABC=S△OAD+S梯形ADEB+S梯形BEFC-S△OFC
=$\frac{1}{2}$×2×5+$\frac{1}{2}$×(5+7)×(7-2)+$\frac{1}{2}$×(7+1)×(9-7)-$\frac{1}{2}$×9×1
=38.5,
(3)当点在第二象限时,即a>0时,
如图4.连接OA,OC,
∵A(2,2)、B(4,0)、C(-2,a),
∴同(1)的方法得出,
S△ABC=$\frac{1}{2}$×4×a-$\frac{1}{2}$×4×2-[$\frac{1}{2}$×(2+a)×(2+2)-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×a]
∵△ABC的面积为12,
∴$\frac{1}{2}$×4×a-[$\frac{1}{2}$×(2+a)×(2+2)-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×a]=12,
∴a=18,
当点在第三象限时,即a<0时,
如图4.连接OA,OC,
∵A(2,2)、B(4,0)、C(-2,a),
∴同(1)的方法得出,
$\frac{1}{2}$×4×2+$\frac{1}{2}$×4×(-a)-[$\frac{1}{2}$(2+2)(2-a)-$\frac{1}{2}$×(2+4)×2-$\frac{1}{2}$×2×(-a)]=12,
∴a=-6,
即:满足条件的a=-6或a=18.
点评 此题是三角形综合题,主要考查了平面坐标系内,几何图形的面积的计算方法,解本题的关键是由前两问找出规律求第三问.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
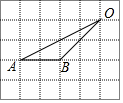 如图,正方形网格中每个小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的余弦值是$\frac{2\sqrt{5}}{5}$.
如图,正方形网格中每个小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的余弦值是$\frac{2\sqrt{5}}{5}$. 数学实验室:
数学实验室: