题目内容
4.已知a,b为常数,若ax+b>0的解集是x>$\frac{1}{3}$,则bx-a<0的解集是x>-3.分析 根据ax+b>0的解集是x>$\frac{1}{3}$,可以解得a、b的值,再代入bx-a<0中求其解集即可.
解答 解:∵ax+b>0的解集是:x>$\frac{1}{3}$,
由于不等号的方向没有发生变化,
∴a>0,又-$\frac{b}{a}$=$\frac{1}{3}$,即a=-3b,
∴b<0,
不等式bx-a<0即bx+3b<0,
解得:x>-3.
点评 本题考查了解简单不等式的能力,解答这类题学生在解题时要注意移项要改变符号这一点.此题解不等式主要依据不等式的基本性质:不等式的两边同时乘以或除以同一个负数不等号的方向改变.正确判断出ab的取值范围及关系是解答此题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
14.若(x-1)2+$\sqrt{x+y}$=0,则x2016+y2017的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |

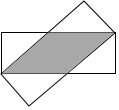 (如图所示)两个长宽分别为7cm、3cm的矩形如图叠放在一起,则图中阴影部分的面积是$\frac{87}{7}$cm2.
(如图所示)两个长宽分别为7cm、3cm的矩形如图叠放在一起,则图中阴影部分的面积是$\frac{87}{7}$cm2.