题目内容
19.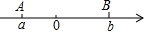 数学实验室:
数学实验室:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
利用数形结合思想回答下列问题:
①数轴上表示2和6两点之间的距离是4,数轴上表示1和-4的两点之间的距离是5.
②数轴上表示x和-3的两点之间的距离表示为|x+3|.数轴上表示x和6的两点之间的距离表示为|x-6|.
③若x表示一个有理数,则|x-1|+|x+4|的最小值=5.
④若x表示一个有理数,且|x+1|+|x-3|=4,则满足条件的所有整数x的是-1或0或1或2或3.
⑤若x表示一个有理数,当x为3,式子|x+2|+|x-3|+|x-4|有最小值为6.
分析 ①数轴上两点间的距离等于两个数的差的绝对值;
②数轴上两点间的距离等于两个数的差的绝对值;
③根据绝对值几何意义即可得出结论.
④分情况讨论计算即可得出结论;
⑤|x+2|+|x-3|+|x-4|表示数轴上某点到表示-2、3、4三点的距离之和,
解答 解:①数轴上表示2和6两点之间的距离是|6-2|=4,
数轴上表示1和-4的两点之间的距离是|1-(-4)|=5;
故答案为:4,5;
②数轴上表示x和-3的两点之间的距离表示为|x-(-3)|=|x+3|,
数轴上表示x和6的两点之间的距离表示为|x-6|;
故答案为:|x+3|,|x-6|;
③根据绝对值的定义有:|x-1|+|x+4|可表示为点x到1与-4两点距离之和,根据几何意义分析可知:
当x在-4与1之间时,|x-1|+|x+4|有最小值5,
故答案为:5;
④当x<-1时,|x+1|+|x-3|=-x-1+3-x=-2x+2=4,
解得:x=-1,
此时不符合x<-1,舍去;
当-1≤x≤3时,|x+1|+|x-3|=x+1+3-x=4,
此时x=-1或x=0,x=1,x=2,x=3;
当x>3时,|x+1|+|x-3|=x+1+x-3=2x-2=4,
解得:x=3,
此时不符合x>3,舍去;
故答案为:-1或0或1或2或3;
⑤:∵可看作是数轴上表示x的点到-2、3、4三点的距离之和,
∴当x=3时,|x+2|+|x-3|+|x-4|有最小值.
∴|x+2|+|x-3|+|x-4|的最小值=|3+2|+|3-3|+|3-4|=6.
故答案为3,6.
点评 此题是绝对值题目,主要考查的是绝对值的应用,明确|x+2|+|x-3|+|x-4|的几何意义是解题的关键.

练习册系列答案
相关题目
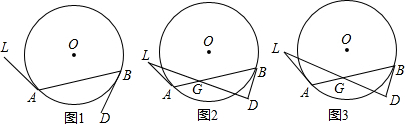
4. 如图1,圆的周长为4个单位,在该圆的4等分点处分别标上字母m、n、p、q,如图2,先让圆周上表示m的点与数轴原点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示-2016的点与圆周上重合的点对应的字母是( )
如图1,圆的周长为4个单位,在该圆的4等分点处分别标上字母m、n、p、q,如图2,先让圆周上表示m的点与数轴原点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示-2016的点与圆周上重合的点对应的字母是( )
 如图1,圆的周长为4个单位,在该圆的4等分点处分别标上字母m、n、p、q,如图2,先让圆周上表示m的点与数轴原点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示-2016的点与圆周上重合的点对应的字母是( )
如图1,圆的周长为4个单位,在该圆的4等分点处分别标上字母m、n、p、q,如图2,先让圆周上表示m的点与数轴原点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示-2016的点与圆周上重合的点对应的字母是( )| A. | m | B. | n | C. | p | D. | q |
11.我区某中学为便于管理,决定给每个学生编号,设定末尾用1表示男生,2表示女生.如果编号0903231表示“2009年入学的3班23号学生,是位男生”,那么2016年入学的10班20号女生同学的编号为( )
| A. | 1016201 | B. | 1601202 | C. | 1610201 | D. | 1610202 |
8.七(1)班男生有a人,女生人数比男生人数的一半多4人,则女生人数是( )
| A. | $\frac{1}{2}$(a+4) | B. | $\frac{1}{2}$(a-4) | C. | $\frac{1}{2}$a+4 | D. | $\frac{1}{2}$a-4 |
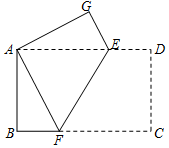 长方形具有四个内角均为直角,并且两组对边分别相等的特征.如图,把一张长方形纸片ABCD折叠,使点C与点A重合,折痕为EF.
长方形具有四个内角均为直角,并且两组对边分别相等的特征.如图,把一张长方形纸片ABCD折叠,使点C与点A重合,折痕为EF.