题目内容
15.若最简二次根式$\frac{2}{3}$$\sqrt{3{m}^{2}-2}$与$\root{{n}^{2}-1}{4{m}^{2}-10}$是同类二次根式,求m2+n2的值.分析 根据同类二次根式,可得方程组,根据解方程组,可得m、n的值,根据实数的运算,可得答案.
解答 解:由最简二次根式$\frac{2}{3}$$\sqrt{3{m}^{2}-2}$与$\root{{n}^{2}-1}{4{m}^{2}-10}$是同类二次根式,得
$\left\{\begin{array}{l}{3{m}^{2}-2=4{m}^{2}-10}\\{{n}^{2}-1=2}\end{array}\right.$.
解得$\left\{\begin{array}{l}{{m}^{2}=8}\\{{n}^{2}=3}\end{array}\right.$.
m2+n2=8+3=11.
点评 本题考查了同类二次根式,利用同类二次根式得出方程组是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.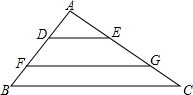 如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )
如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )
 如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )
如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )| A. | 1:2 | B. | 1:4 | C. | 1:$\sqrt{3}$ | D. | 1:$\sqrt{2}$ |
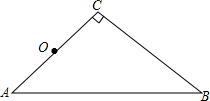 在等腰直角三角形ABC中,∠C=90°,BC=2cm.以AC的中点O为对称中心,画出与△ABC关于点O成中心对称的△DEF,点A、B、C的对称点分别是点D、E、F,并求出BE的长.
在等腰直角三角形ABC中,∠C=90°,BC=2cm.以AC的中点O为对称中心,画出与△ABC关于点O成中心对称的△DEF,点A、B、C的对称点分别是点D、E、F,并求出BE的长. 如图,将平行四边形ABCD折叠,使点A与C重合,折痕为EF.若∠A=60,AD=4,AB=6,则AE为$\frac{19}{4}$.
如图,将平行四边形ABCD折叠,使点A与C重合,折痕为EF.若∠A=60,AD=4,AB=6,则AE为$\frac{19}{4}$.