题目内容
5.解下列不等式组,并把解集在数轴上表示出来.(1)$\left\{\begin{array}{l}{x-1>0}\\{3(x+2)<5x}\end{array}\right.$
(2)$\left\{\begin{array}{l}{6x+15>2(4x+3)}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$.
分析 (1)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)$\left\{\begin{array}{l}{x-1>0①}\\{3(x+2)<5x②}\end{array}\right.$
解①得x>1,
解②得x>3,
故此不等式组的解集为:x>3;
在数轴上表示为:
(2)$\left\{\begin{array}{l}{6x+15>2(4x+3)①}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}②}\end{array}\right.$
解①得x$<\frac{9}{2}$,
解②得x≥-2,
故此不等式组的解集为:-2≤x<$\frac{9}{2}$.
在数轴上表示为:
点评 本题考查的是解一元一次不等式组,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
16.下图是小红在某路口统计20分钟各种车辆通过情况制成的统计表,其中空格处的字迹已模糊,但小红还记得
7:50~8:00时段内的电瓶车车辆与8:00~8:10时段内的货车车辆数之比是7:2
(1)若在7:50~8:00时段,经过的小轿车数量正好是电瓶车数量的$\frac{9}{8}$,求这个时段内的电瓶车通过的车辆数;
(2)根据上述表格数据,求在7:50~8:00和8:00~8:10两个时段内电瓶车和货车的车辆数;
(3)据估计,在所调查的7:50~8:00时段内,每增加1辆公交车,可减少8辆小轿车行驶,为了使该时段内小轿车流量减少到比公交车多13辆,则在该路口应再增加几辆公交车.
7:50~8:00时段内的电瓶车车辆与8:00~8:10时段内的货车车辆数之比是7:2
| 电瓶车 | 公交车 | 货车 | 小轿车 | 合计 | |
| 7:50~8:00 | 5 | 63 | 138 | ||
| 8:00~8:10 | 5 | 45 | 77 | ||
| 合计 | 67 | 30 | 108 |
(2)根据上述表格数据,求在7:50~8:00和8:00~8:10两个时段内电瓶车和货车的车辆数;
(3)据估计,在所调查的7:50~8:00时段内,每增加1辆公交车,可减少8辆小轿车行驶,为了使该时段内小轿车流量减少到比公交车多13辆,则在该路口应再增加几辆公交车.
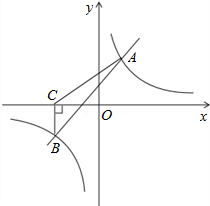 如图,函数y=x+b与y=$\frac{k}{x}$相交于点A(2,n)和点B(3-2n,-2).
如图,函数y=x+b与y=$\frac{k}{x}$相交于点A(2,n)和点B(3-2n,-2).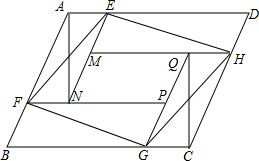 如图,有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ,连接EF、GH得到四边形EFGH,设S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,则S2=$\frac{10}{3}$.
如图,有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ,连接EF、GH得到四边形EFGH,设S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,则S2=$\frac{10}{3}$. 如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,连接EC,则∠BCE=65°.
如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,连接EC,则∠BCE=65°. 如图所示,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,问:∠1和∠2相等吗?请说明理由.
如图所示,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,问:∠1和∠2相等吗?请说明理由.