题目内容
6. 如图,将平行四边形ABCD折叠,使点A与C重合,折痕为EF.若∠A=60,AD=4,AB=6,则AE为$\frac{19}{4}$.
如图,将平行四边形ABCD折叠,使点A与C重合,折痕为EF.若∠A=60,AD=4,AB=6,则AE为$\frac{19}{4}$.
分析 作CM⊥AB于M,由平行四边形的性质得出BC=AD=4,BC∥AD,得出∠CBM=∠A=60°,由三角函数求出BM、CM,设AE=x,则BE=6-x,EM=8-x,根据勾股定理得出方程,解方程即可求出AE的长.
解答 解:作CM⊥AB于M,如图所示: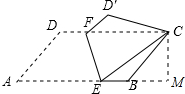
则∠M=90°,
∵四边形ABCD是平行四边形,
∴BC=AD=4,BC∥AD,
∴∠CBM=∠A=60°,
∴BM=BC•cos60°=4×$\frac{1}{2}$=2,CM=BC•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
设AE=x,则BE=6-x,EM=8-x,
∵CE2=CM2+EM2,
∴x2=(2$\sqrt{3}$)2+(8-x)2,
解得:x=$\frac{19}{4}$,
∴AE=$\frac{19}{4}$.
故答案为:$\frac{19}{4}$.
点评 本题考查了平行四边形的性质、翻折变换、勾股定理以及三角函数;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知三角形的两边长是2cm,3cm,则该三角形的周长l的取值范围是( )
| A. | 1<l<5 | B. | 1<l<6 | C. | 5<l<9 | D. | 6<l<10 |
16.下图是小红在某路口统计20分钟各种车辆通过情况制成的统计表,其中空格处的字迹已模糊,但小红还记得
7:50~8:00时段内的电瓶车车辆与8:00~8:10时段内的货车车辆数之比是7:2
(1)若在7:50~8:00时段,经过的小轿车数量正好是电瓶车数量的$\frac{9}{8}$,求这个时段内的电瓶车通过的车辆数;
(2)根据上述表格数据,求在7:50~8:00和8:00~8:10两个时段内电瓶车和货车的车辆数;
(3)据估计,在所调查的7:50~8:00时段内,每增加1辆公交车,可减少8辆小轿车行驶,为了使该时段内小轿车流量减少到比公交车多13辆,则在该路口应再增加几辆公交车.
7:50~8:00时段内的电瓶车车辆与8:00~8:10时段内的货车车辆数之比是7:2
| 电瓶车 | 公交车 | 货车 | 小轿车 | 合计 | |
| 7:50~8:00 | 5 | 63 | 138 | ||
| 8:00~8:10 | 5 | 45 | 77 | ||
| 合计 | 67 | 30 | 108 |
(2)根据上述表格数据,求在7:50~8:00和8:00~8:10两个时段内电瓶车和货车的车辆数;
(3)据估计,在所调查的7:50~8:00时段内,每增加1辆公交车,可减少8辆小轿车行驶,为了使该时段内小轿车流量减少到比公交车多13辆,则在该路口应再增加几辆公交车.
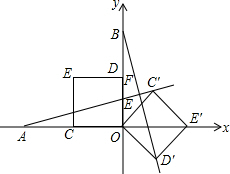 如图,在平面直角坐标系中,O为原点,点A的坐标为(-4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a<360°),连结AC′、BD′,设直线AC′与直线BD′相交于点F,则点F的纵坐标的最大值为$\sqrt{3}$+1.
如图,在平面直角坐标系中,O为原点,点A的坐标为(-4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a<360°),连结AC′、BD′,设直线AC′与直线BD′相交于点F,则点F的纵坐标的最大值为$\sqrt{3}$+1.