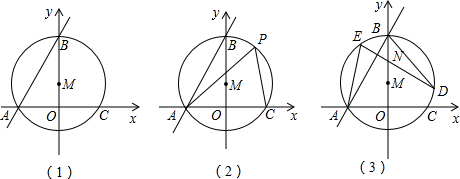题目内容
7.一次函数y=kx+b的图象与反比例函数y=$\frac{-2}{x}$的图象相交于A(-1,m),B(n,-1)两点.(1)写出这个一次函数的表达式;
(2)画出函数图象草图,并据此写出使一次函数值大于反比例函数值的x的取值范围.
分析 (1)先把A(-1,m),B(n,-1)分别代入反比例函数解析式可求出m、n,于是确定A点坐标为(-1,2),B点坐标为(2,-1),然后利用待定系数法求直线AB的解析式;
(2)根据函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
解答 解:(1)把A(-1,m),B(n,-1)分别代入y=$\frac{-2}{x}$,
得-m=-2,-n=-2,解得m=2,n=2,
所以A点坐标为(-1,2),B点坐标为(2,-1),
把A(-1,2),B(2,-1)代入y=kx+b得$\left\{\begin{array}{l}{-k+b=2}\\{2k+b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
所以这个一次函数的表达式为y=-x+1;
(2)当x<-1或0<x<2时,一次函数的值大于反比例函数的值.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.

练习册系列答案
相关题目
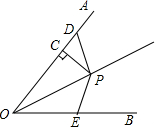 如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.
如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.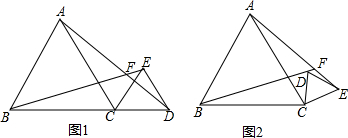
 已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.
已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.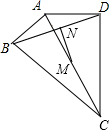 如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,AC=26,BD=24,则线段MN长为5.
如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,AC=26,BD=24,则线段MN长为5.