题目内容
12.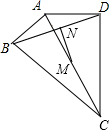 如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,AC=26,BD=24,则线段MN长为5.
如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,AC=26,BD=24,则线段MN长为5.
分析 根据在直角三角形中,斜边上的中线等于斜边的一半得到BM=DM=5,根据等腰三角形的性质得到BN=4,根据勾股定理得到答案.
解答  解:连接BM、DM,
解:连接BM、DM,
∵∠ABC=∠ADC=90°,M是AC的中点,
∴BM=$\frac{1}{2}$AC,DM=$\frac{1}{2}$AC,
∴BM=DM=13,又N是BD的中点,
∴BN=DN=$\frac{1}{2}$BD=12,
∴MN=$\sqrt{B{M}^{2}-B{N}^{2}}$=5,
故答案为:5.
点评 本题考查的是直角三角形的性质、等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
2.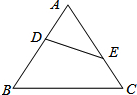 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )| A. | 3 | B. | 12 | C. | $\frac{25}{3}$ | D. | 7 |
4.若-2amb5与5a2bn-1可以合并成一项,则nm的值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 64 |

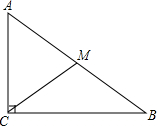 如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,CM是中线,以2.5cm为半径画⊙C,试判断A、B、M三点与⊙C的位置关系.
如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,CM是中线,以2.5cm为半径画⊙C,试判断A、B、M三点与⊙C的位置关系.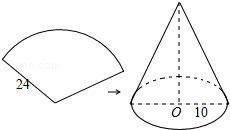 如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是240πcm2.
如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是240πcm2.