题目内容
16.计算:(1)($\sqrt{6}$$-\sqrt{\frac{1}{2}}$)×($\sqrt{24}$$+2\sqrt{\frac{2}{3}}$)
(2)($\sqrt{6}$$-2\sqrt{15}$)×$\sqrt{3}-6\sqrt{\frac{1}{2}}$
(3)($\sqrt{3}+1$)2
(4)$\sqrt{8}$$+\sqrt{32}$$+\sqrt{18}$$-\sqrt{24}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并后进行二次根式的乘法运算;
(2)先根据二次根式的乘法法则运算,然后化简后合并即可;
(3)利用完全平方公式计算;
(4)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=($\sqrt{6}$-$\frac{\sqrt{2}}{2}$)×(2$\sqrt{6}$+$\frac{2\sqrt{6}}{3}$)
=($\sqrt{6}$-$\frac{\sqrt{2}}{2}$)×$\frac{8\sqrt{6}}{3}$
=$\sqrt{6}$×$\frac{8\sqrt{6}}{3}$-$\frac{\sqrt{2}}{2}$×$\frac{8\sqrt{6}}{3}$
=16-$\frac{8\sqrt{3}}{3}$;
(2)原式=$\sqrt{6×3}$-2$\sqrt{15×3}$-3$\sqrt{2}$
=3$\sqrt{2}$-6$\sqrt{5}$-3$\sqrt{2}$
=-6$\sqrt{5}$;
(3)原式=3+2$\sqrt{3}$+1
=4+2$\sqrt{3}$;
(4)原式=2$\sqrt{2}$+4$\sqrt{2}$+3$\sqrt{2}$-2$\sqrt{6}$
=9$\sqrt{2}$-2$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
6.已知-1是关于x的方程x2+4x-m=0的一个根,则这个方程的另一个根是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
4.若-2amb5与5a2bn-1可以合并成一项,则nm的值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 64 |
 如图,△ABC的中线BE,CF相交于点G,证明:BG=2GE,CG=2GF.
如图,△ABC的中线BE,CF相交于点G,证明:BG=2GE,CG=2GF.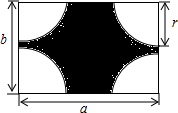 如图,有一块长为a米,宽为b米的长方形铁皮,将四个角分别截去半径都是r米的四分之一的圆形.
如图,有一块长为a米,宽为b米的长方形铁皮,将四个角分别截去半径都是r米的四分之一的圆形.