题目内容
16.我们给出如下定义:若一个四边形的有一组对边相等,另一组对边不相等,则称这个四边形为等对边四边形.(1)写出你所学过的特殊四边形中是等对边四边形的一种图形的名称;
(2)请你探究:等对边四边形另一组对边中点的连线段与等对边中一条线段长度的大小关系,并证明你的结论.(写出已知、求证与证明)
分析 (1)根据题目中的定义即刻得到结论;
(2)连接AC,取AC的中点G,连接EG,FG,根据三角形中位线的性质和三角形的三边关系即可得到结论.
解答 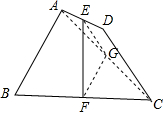 解:(1)所学过的特殊四边形中是等对边四边形的一种图形的名称:等腰梯形;
解:(1)所学过的特殊四边形中是等对边四边形的一种图形的名称:等腰梯形;
(2)另一组对边中点的连线段小于等对边中一条线段长度;
已知:四边形ABCD,AB=CD,点E,F分别是AD,BC的中点,
求证:EF<AB,
证明:连接AC,取AC的中点G,连接EG,FG,
∵点E,F分别是AD,BC的中点,
∴AE=DE,BF=CF,
∴EG=$\frac{1}{2}$CD,GF=$\frac{1}{2}$AB,
∵AB=CD,
∴GE+GF=AB=CD,
在△EFG中,EG+FG>EF,
∴AB>EF.
点评 本题考查了三角形的中位线的性质,等腰梯形的性质,正确的作出图形是解题的关键.

练习册系列答案
相关题目
5.方程x2=x的解是( )
| A. | x=1 | B. | x=0 | C. | x1=1 x2=0 | D. | x1=-1 x2=0 |
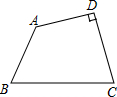 如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD=$\sqrt{6}$.
如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD=$\sqrt{6}$.
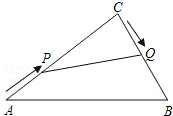 在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求:
在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求: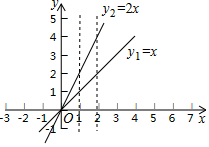 小华在研究函数y1=x与y2=2x图象关系时发现:如图所示,当x=1时,y1=1,y2=2;当x=2时,y1=2,y2=4;…;当x=a时,y1=a,y2=2a.他得出如果将函数y1=x图象上各点的横坐标不变,纵坐标变为原来的2倍,就可以得到函数y2=2x的图象.类比小华的研究方法,解决下列问题:
小华在研究函数y1=x与y2=2x图象关系时发现:如图所示,当x=1时,y1=1,y2=2;当x=2时,y1=2,y2=4;…;当x=a时,y1=a,y2=2a.他得出如果将函数y1=x图象上各点的横坐标不变,纵坐标变为原来的2倍,就可以得到函数y2=2x的图象.类比小华的研究方法,解决下列问题: 如图,在平面直角坐标系xOy中,正方形ABOD的边OD,BO在坐标轴上,正方形边长为4,直线y=2x+2与y轴交于点E,与x轴交于点F.
如图,在平面直角坐标系xOy中,正方形ABOD的边OD,BO在坐标轴上,正方形边长为4,直线y=2x+2与y轴交于点E,与x轴交于点F.